
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 (几何法)
设AA1=$\sqrt{2}$,AB=1,取A1C1的中点E,连结B1E,AE,则B1E∥BD,∠AB1E是异面直线AB1与BD所成的角(或所成角的补角),由此利用余弦定理能求出异面直线AB1与BD所成的角.
(向量法)
设AA1=$\sqrt{2}$,AB=1,以A为原点,过A在平面ABC内作AC的垂线为x轴,以AC为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能求出异面直线AB1与BD所成的角.
解答 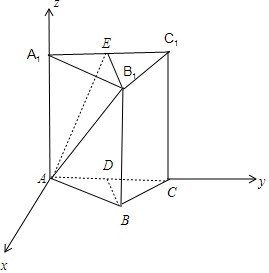 解:(几何法)
解:(几何法)
∵在正棱柱ABC-A1B1C1中,D是AC的中点,AA1:AB=$\sqrt{2}$:1,
∴设AA1=$\sqrt{2}$,AB=1,
取A1C1的中点E,连结B1E,AE,则B1E∥BD,
∴∠AB1E是异面直线AB1与BD所成的角(或所成角的补角),
B1E=$\sqrt{{1}^{2}-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$,AB1=$\sqrt{2+1}=\sqrt{3}$,AE=$\sqrt{2+\frac{1}{4}}$=$\frac{3}{2}$,
∴cos∠AB1E=$\frac{A{{B}_{1}}^{2}+{B}_{1}{E}^{2}-A{E}^{2}}{2A{B}_{1}•{B}_{1}E}$=$\frac{3+\frac{3}{4}-\frac{9}{4}}{2•\sqrt{3}•\frac{\sqrt{3}}{2}}$=$\frac{1}{2}$,
∴∠AB1E=60°,
∴异面直线AB1与BD所成的角为60°.
故选:C.
(向量法)
∵在正棱柱ABC-A1B1C1中,D是AC的中点,AA1:AB=$\sqrt{2}$:1,
∴设AA1=$\sqrt{2}$,AB=1,
以A为原点,过A在平面ABC内作AC的垂线为x轴,以AC为y轴,AA1为z轴,建立空间直角坐标系,
A(0,0,0),B1($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,$\sqrt{2}$),B($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,0),D(0,$\frac{1}{2}$,0),
$\overrightarrow{A{B}_{1}}$=($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,$\sqrt{2}$),$\overrightarrow{BD}$=(-$\frac{\sqrt{3}}{2}$,0,0),
设异面直线AB1与BD所成的角为θ,
则cosθ=$\frac{|\overrightarrow{A{B}_{1}}•\overrightarrow{BD}|}{|\overrightarrow{A{B}_{1}}|•|\overrightarrow{BD}|}$=$\frac{\frac{3}{4}}{\sqrt{3}•\frac{\sqrt{3}}{2}}$=$\frac{1}{2}$,
∴θ=60°,
∴异面直线AB1与BD所成的角为60°.
故选:C.
点评 本题考查异面直线所成角的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | $\frac{24}{5}$ | D. | $\frac{36}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{10}{3}$<λ≤$\frac{9}{4}$ | B. | $-\frac{10}{3}$<λ<$\frac{9}{4}$ | C. | $-\frac{9}{4}$<λ≤$\frac{10}{3}$ | D. | $-\frac{9}{4}$<λ<$\frac{10}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{4}$,0) | B. | ($-\frac{1}{2}$,-$\frac{1}{4}$) | C. | ($-\frac{1}{2}$,$-\frac{1}{4}$)∪($-\frac{1}{4}$,-$\frac{1}{8}$) | D. | (-$\frac{1}{2}$,$-\frac{1}{8}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
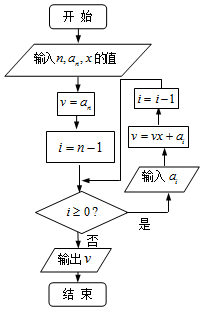 如图程序框图的算法思路,源于我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出的秦九韶算法,执行该程序框图,若输入的n,an,x分别为5,1,-2,且a4=5,a3=10,a2=10,a1=5,a0=1,则输出的v=( )
如图程序框图的算法思路,源于我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出的秦九韶算法,执行该程序框图,若输入的n,an,x分别为5,1,-2,且a4=5,a3=10,a2=10,a1=5,a0=1,则输出的v=( )| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com