
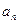 }和{
}和{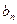 }满足:对于任何
}满足:对于任何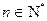 ,有
,有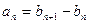 ,
,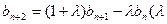 为非零常数),且
为非零常数),且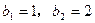 .
.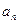 }和{
}和{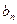 }的通项公式;
}的通项公式;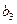 是
是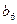 与
与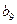 的等差中项,试求
的等差中项,试求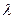 的值,并研究:对任意的
的值,并研究:对任意的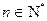 ,
,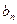 是否一定能是数列{
是否一定能是数列{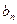 }中某两项(不同于
}中某两项(不同于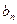 )的等差中项,并证明你的结论.
)的等差中项,并证明你的结论.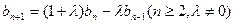 得,
得,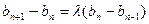 .
.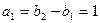 ,
, ,
,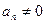 .
.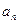 }是首项为1,公比为
}是首项为1,公比为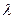 的等比数列,
的等比数列,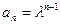 .…………………………….5分
.…………………………….5分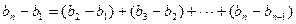 ,得
,得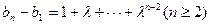
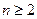 时,
时,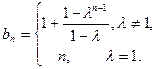 ……………………………………………….6分
……………………………………………….6分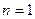 显然成立.………………………………………………………………………..1分
显然成立.………………………………………………………………………..1分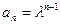 ,并用数学归纳法证明…………………………………………….5分
,并用数学归纳法证明…………………………………………….5分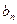 的求法如【解一】 ………………………………………………………………………..7分
的求法如【解一】 ………………………………………………………………………..7分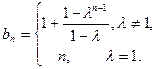 ,并用数学归纳法证明………………………….7分
,并用数学归纳法证明………………………….7分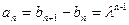 …………………………………………………………………..5分
…………………………………………………………………..5分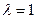 时,
时,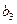 不是
不是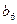 与
与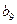 的等差中项,不合题意;……………………………….1分
的等差中项,不合题意;……………………………….1分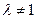 时,由
时,由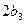
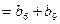 得
得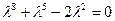 ,
, 得
得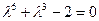 (可解得
(可解得 )..…………………………………………2分
)..…………………………………………2分 ,
,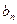 是
是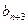 与
与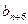 的等差中项. .………………………………….2分
的等差中项. .………………………………….2分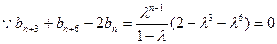 ,
,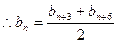 , .………………………………….3分
, .………………………………….3分 ,
,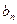 是
是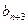 与
与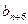 的等差中项.
的等差中项.

科目:高中数学 来源:不详 题型:解答题
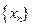 的前n项和为
的前n项和为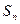 满足
满足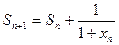 ,
,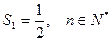
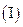 猜想数列
猜想数列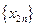 的单调性,并证明你的结论;
的单调性,并证明你的结论;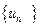 若存在常数M>0,对任意的
若存在常数M>0,对任意的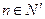 ,恒有
,恒有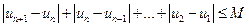

 ,, 则称数列
,, 则称数列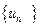 为B-数列。问数列
为B-数列。问数列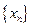 是B-数列吗? 并证明你的结论。
是B-数列吗? 并证明你的结论。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
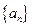 满足:
满足: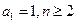 时,
时,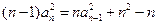 。
。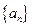 的通项公式;
的通项公式;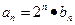 ,数列
,数列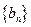 的前n项和为
的前n项和为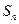 ,是否存在正整数m,使得对任意的
,是否存在正整数m,使得对任意的
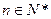 ,
,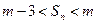 恒成立?若存在,求出所有的正整数m;若不存在,说明理由。
恒成立?若存在,求出所有的正整数m;若不存在,说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.13项 | B.12项 | C.11项 | D.10项 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 前2012项之和S2012等于________.
前2012项之和S2012等于________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
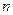 行有
行有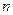 个数且两端的数均为
个数且两端的数均为
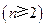 ,每个数是它下一行左右相邻两数的和,如
,每个数是它下一行左右相邻两数的和,如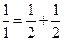 ,
, ,
,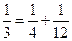 ,…,则第7行第4个数(从左往右数)为( )
,…,则第7行第4个数(从左往右数)为( )
A.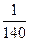 | B.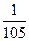 | C.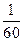 | D.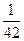 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
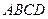 分割成
分割成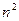
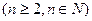 个全等的小正方形(图1,图2分别给出了
个全等的小正方形(图1,图2分别给出了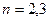 的情形),在每个小正方形的顶点各放置一个数,使位于正方形
的情形),在每个小正方形的顶点各放置一个数,使位于正方形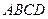 的四边及平行于某边的任一直线上的数都分别依次成等差数列,若顶点
的四边及平行于某边的任一直线上的数都分别依次成等差数列,若顶点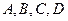 处的四个数互不相同且和为1,记所有顶点上的数之和为
处的四个数互不相同且和为1,记所有顶点上的数之和为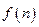 ,则
,则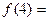
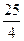 .
.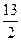
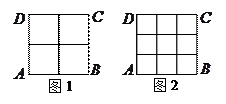
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com