
【题目】某商场销售某种品牌的空调器,每周周初购进一定数量的空调器,商场每销售一台空调器可获利500元,若供大于求,则每台多余的空调器需交保管费100元;若供不应求,则可从其他商店调剂供应,此时每台空调器仅获利润200元。
(Ⅰ)若该商场周初购进20台空调器,求当周的利润(单位:元)关于当周需求量n(单位:台,![]() )的函数解析式
)的函数解析式![]() ;
;
(Ⅱ)该商场记录了去年夏天(共10周)空调器需求量n(单位:台),整理得下表:
周需求量n | 18 | 19 | 20 | 21 | 22 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10周记录的各需求量的频率作为各需求量发生的概率,若商场周初购进20台空调器,X表示当周的利润(单位:元),求X的分布列及数学期望。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】假设要考察某公司生产的流感疫苗的剂量是否达标,现从500支疫苗中抽取50支进行检验,利用随机数表法抽取样本时,先将500支疫苗按![]() 进行编号,如果从随机数表第7行第8列的数开始向右读,请写出第3支疫苗的编号________.(下面摘取了随机数表第7行至第9行)
进行编号,如果从随机数表第7行第8列的数开始向右读,请写出第3支疫苗的编号________.(下面摘取了随机数表第7行至第9行)
第7行:84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50
25 83 92 12 06 76
第8行:63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58
07 44 39 52 38 79
第9行:33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13
42 99 66 02 79 54
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若两个椭圆的离心率相等,则称两个椭圆是“相似”的,如图,椭圆![]() 与椭圆
与椭圆![]() 是相似的两个椭圆,并且相交于上下两个顶点,椭圆
是相似的两个椭圆,并且相交于上下两个顶点,椭圆![]() 的长轴长是4,椭圆
的长轴长是4,椭圆![]() ,短轴长是1,点
,短轴长是1,点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左焦点与右焦点.
的左焦点与右焦点.

(1)求椭圆![]() ,
,![]() 的方程;
的方程;
(2)过![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() ,
,![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
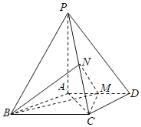
(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求四面体N-BCM的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了对某课题进行讨论研究,用分层抽样的方法从三所高校A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
高校 | 相关人数 | 抽取人数 |
A | x | 1 |
B | 36 | y |
C | 54 | 3 |
(1)求x、y;
(2)若从高校B相关的人中选2人作专题发言,应采用什么抽样法,请写出合理的抽样过程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱锥S-ABCD中,O为顶点在底面内的投影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC的夹角是

A. 30°B. 45°C. 60°D. 90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.

(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B–EC–C1的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 若命题![]() 都是真命题,则命题“
都是真命题,则命题“![]() ”为真命题
”为真命题
B. 命题“![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
C. 命题:“若![]() ,则
,则![]() 或
或![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() 或
或![]() ”
”
D. “![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理是类比推理的( )
A. 两条直线平行,同旁内角互补,如果![]() 和
和![]() 是两条平行直线的同旁内角,则
是两条平行直线的同旁内角,则![]()
B. 由平面三角形的性质,推测空间四边形的性质
C. 某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员.
D. 一切偶数都能被2整除,![]() 是偶数,所以
是偶数,所以![]() 能被2整除.
能被2整除.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com