
 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2007年普通高等学校招生全国统一考试理科数学卷(重庆) 题型:解答题
(本小题满分13分)某单位有三辆汽车参加某种事故保险,单位年初向保险公司
缴纳每辆900元的保险金.对在一年内发生此种事故的每辆汽车,单位获9000元
的赔偿(假设每辆车最多只赔偿一次)。设这三辆车在一年内发生此种事故的概率
分别为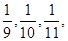 且各车是否发生事故相互独立,求一年内该单位在此保险中:
且各车是否发生事故相互独立,求一年内该单位在此保险中:
(1)获赔的概率;(4分)
(2)获赔金额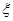 的分别列与期望。(9分)
的分别列与期望。(9分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com