
| 序号 | 前提 | p | q |
| ① | 在区间I上函数f(x)的最小值为m,g(x)的最大值为n | m>n | f(x)>g(x)在区 间I上恒成立 |
| ② | 函数f(x)的导函数为f′(x) | f′(x)>0在区间I上恒成立 | f(x) 在区间I 上单调递增 |
| ③ | A、B为△ABC的两内角 | A>B | sinA>sinB |
| ④ | 两平面向量 、 、 |  |  、 、 的夹角为钝角 的夹角为钝角 |
| ⑤ | 直线l1:A1x+B1y+C1=0l2:A2x+B2y+C2=0 |  | l1∥l2 |
 )?sinA>sinB,所以③不满足要求.
)?sinA>sinB,所以③不满足要求. <0?|
<0?| ||
|| |cos
|cos <0?cos
<0?cos <0?
<0? 、
、 的夹角为钝角.所以④不满足要求.
的夹角为钝角.所以④不满足要求.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
| 序号 | 前提 | p | q | ||||||||||||
| ① | 在区间I上函数f(x)的最小值为m,g(x)的最大值为n | m>n | f(x)>g(x)在区 间I上恒成立 | ||||||||||||
| ② | 函数f(x)的导函数为f′(x) | f′(x)>0在区间I上恒成立 | f(x) 在区间I 上单调递增 | ||||||||||||
| ③ | A、B为△ABC的两内角 | A>B | sinA>sinB | ||||||||||||
| ④ | 两平面向量
|
|
| ||||||||||||
| ⑤ | 直线l1:A1x+B1y+C1=0l2:A2x+B2y+C2=0 |
|
l1∥l2 |
查看答案和解析>>
科目:高中数学 来源:湖北模拟 题型:填空题
| 序号 | 前提 | p | q | ||||||||||||
| ① | 在区间I上函数f(x)的最小值为m,g(x)的最大值为n | m>n | f(x)>g(x)在区 间I上恒成立 | ||||||||||||
| ② | 函数f(x)的导函数为f′(x) | f′(x)>0在区间I上恒成立 | f(x) 在区间I 上单调递增 | ||||||||||||
| ③ | A、B为△ABC的两内角 | A>B | sinA>sinB | ||||||||||||
| ④ | 两平面向量
|
|
| ||||||||||||
| ⑤ | 直线l1:A1x+B1y+C1=0l2:A2x+B2y+C2=0 |
|
l1∥l2 |
查看答案和解析>>
科目:高中数学 来源:模拟题 题型:解答题
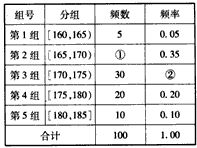
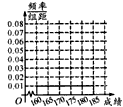
查看答案和解析>>
科目:高中数学 来源: 题型:
如下表,在相应各前提下,满足p是q的充分不必要条件所对应的序号有
(填出所有满足要求的序号).
| 序号 | 前提 | p | q |
| ① | 在区间I上函数f(x)的最小值为m, g(x)的最大值为n | m>n | f(x)>g(x)在区 间I上恒成立 |
| ② | 函数f(x)的导函数为f′(x) | f′(x)>0在区间I上恒成立 | f(x) 在区间I 上单调递增 |
| ③ | A、B为△ABC的两内角 | A>B | sinA>sinB |
| ④ | 两平面向量 |
|
|
| ⑤ | 直线
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com