
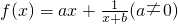 的图象过点(0,-1)且与直线y=-1有且只有一个公共点;设点P(x0,y0)是函数y=f(x)图象上任意一点,过点P分别作直线y=x和直线x=1的垂线,垂足分别是M,N.
的图象过点(0,-1)且与直线y=-1有且只有一个公共点;设点P(x0,y0)是函数y=f(x)图象上任意一点,过点P分别作直线y=x和直线x=1的垂线,垂足分别是M,N.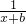 (a≠0)的图象过点(0,-1)
(a≠0)的图象过点(0,-1) ,
, 只有一解即x[ax+(a-1)]=0只有一解∴a=1
只有一解即x[ax+(a-1)]=0只有一解∴a=1
 都是奇函数.
都是奇函数. 也是奇函数,其图象是以原点为中心的中心对称图形.
也是奇函数,其图象是以原点为中心的中心对称图形. +1
+1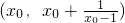
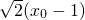 .
.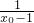 ,∴PB=PA-AB=
,∴PB=PA-AB=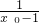 ,
, .
.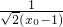 .(x0-1)=
.(x0-1)= 为定值.
为定值.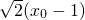 +
+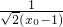 ,
,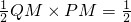 ×
×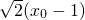 +
+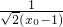 ].
].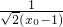 =
=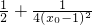
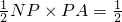 (x0-1).(x0-1+
(x0-1).(x0-1+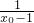 )=
)=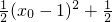
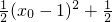 +
+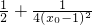 =
=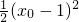 +
+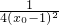 +1
+1

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
A、(
| ||
B、(1,
| ||
| C、(1,0) | ||
| D、(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | x |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求![]() 的表达式;
的表达式;
(2)是否存在正实数p,使F(x)在(-∞,f(2)]上是增函数,在(f(2),0)上是减函数?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com