
已知{an}为等差数列,且a1+a3=8,a2+a4=12.
(1){an}的通项公式;
(2)记{an}的前n项和为Sn,若a1,ak,Sk+2成等比数列,求正整数k的值.
(1) an=2n.(2) k=6.
解析试题分析:(1)利用等差数列的通项公式,借助于条件a1+a3=12,a2+a4=6,可求a1,d的值,从而可求 数列的通项公式an及它的前n项和Sn.
(2)由(1)可得Sn=n(n+1),那么结合因为a1,ak,Sk+2成等比数列得到k的值。
解:(1)设数列{an}的公差为d,由题意知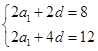 解得a1=2,d=2.
解得a1=2,d=2.
所以an=a1+(n-1)d=2+2(n-1)=2n.
(2)由(1)可得Sn=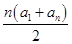 =
=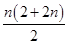 =n(n+1).
=n(n+1).
因为a1,ak,Sk+2成等比数列,所以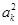 =a1Sk+2.
=a1Sk+2.
从而(2k)2=2(k+2)(k+3),即k2-5k-6=0,
解得k=6或k=-1(舍去).因此k=6.
考点:本试题主要考查了等差数列的通项公式、等比数列的通项公式和前n项和公式,是基础题.解题时要认真审题,正确运用公式。
点评:解决该试题的关键是对于等差数列的等差中项的性质的灵活运用求解通项公式。


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:解答题
将数列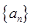 的各项按照第1行排
的各项按照第1行排 ,第2行自左至右排
,第2行自左至右排 ,第3行…的规律,排成如图所示的三角形形状.
,第3行…的规律,排成如图所示的三角形形状.
(Ⅰ)若数列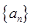 是首项为1,公差为3的等差数列,写出图中第五行第五个数;
是首项为1,公差为3的等差数列,写出图中第五行第五个数;
(Ⅱ)若函数 且
且 ,求数列
,求数列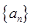 的通项公式;
的通项公式;
(Ⅲ)设 为图中第
为图中第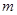 行所有项的和,在(Ⅱ)的条件下,用含
行所有项的和,在(Ⅱ)的条件下,用含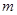 的代数式表示
的代数式表示 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设数列 的首项
的首项 ,前
,前 项和
项和 满足关系式:
满足关系式: 
(1)求证:数列 是等比数列;
是等比数列;
(2)设数列 是公比为
是公比为 ,作数列
,作数列 ,使
,使
 ,
,
求和: ;
;
(3)若 ,设
,设 ,
, ,
,
求使
 恒成立的实数k的范围.
恒成立的实数k的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com