练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    椭圆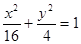上的两个焦点是F1、F2 ，弦AB过焦点F1,，则△ABF2的周长为（    ）

    A．8             B．16         C．32          D．不能确定

     

    【答案】

    B

    【解析】

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知，椭圆C过点A(1，
    32
    )    ，两个焦点为（-1，0），（1，0）．
    （1）求椭圆C的方程；
    （2）E，F是椭圆C上的两个动点，如果直线AE的斜率与AF的斜率互为相反数，证明直线EF的斜率为定值，并求出这个定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

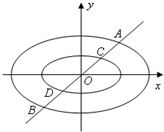    精英家教网定义：由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”．如果两个椭圆的“特征三角形”是相似的，则称这两个椭圆是“相似椭圆”，并将三角形的相似比称为椭圆的相似比．已知椭圆C1：
    x2
    4
    +y2=1    ．
    （1）若椭圆C2：
    x2
    16
    +
    y2
    4
    =1    ，判断C2与C1是否相似？如果相似，求出C2与C1的相似比；如果不相似，请说明理由；
    （2）写出与椭圆C1相似且短半轴长为b的椭圆Cb的方程；若在椭圆Cb上存在两点M、N关于直线y=x+1对称，求实数b的取值范围？
    （3）如图：直线y=x与两个“相似椭圆”M：
    x2
    a2
    +
    y2
    b2
    =1    和Mλ：
    x2
    a2
    +
    y2
    b2
    =λ2(a＞b＞0，0＜λ＜1)    分别交于点A，B和点C，D，试在椭圆M和椭圆Mλ上分别作出点E和点F（非椭圆顶点），使△CDF和△ABE组成以λ为相似比的两个相似三角形，写出具体作法．（不必证明）

    查看答案和解析>>

    科目：高中数学 来源：学习周报　数学　人教课标高二版(A选修1－1)　2009－2010学年　第17期　总第173期 人教课标版(A选修1－1) 题型：044

    如图，A，B是椭圆＋＝1(a＞b＞0)上的两个顶点，F是右焦点，若AB⊥BF，求椭圆的离心率．

    查看答案和解析>>

    科目：高中数学 来源：学习周报　数学　人教课标高二版(A选修2－1)　2009－2010学年　第17期　总第173期 人教课标版(A选修2－1) 题型：044

    如图，A，B是椭圆＝1(a＞b＞0)上的两个顶点，F是右焦点，若AB⊥BF，求椭圆的离心率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆的中心在原点,对称轴为坐标轴,左、右焦点分别为

    是椭圆上的一点，的周长为6，离心率为.

    （1）求椭圆的方程；

    （2）为椭圆上的定点，E,F是椭圆上的两个动点，如果直线AE的斜率与AF的斜率

    互为相反数，证明直线EF的斜率为定值，并求出这个定值。 

    查看答案和解析>>

    同步练习册答案