已知经过点A(-2,0),且以(λ,1+λ)为方向向量的直线l1与经过点B(2,0),且以(1+λ,-3λ)为方向向量的直线l2相交于点P,其中λ∈R.
(1)求点P的轨迹C的方程;
(2)是否存在直线l:y=kx+m(m≠0)与轨迹C相交于不同的两点M、N,且满足|BM|=|BN|?若存在,求出m的取值范围;若不存在,请说明理由.
【答案】
分析:(1)对λ进行讨论,即可求点P的轨迹C的方程;
(2)假设存在直线l:y=kx+m(m≠0)与轨迹C相交于不同的两点M、N,且满足|BM|=|BN|,求出线段MN的中点M
的坐标,利用M
在椭圆C的内部,在直线l上,即可求得结论.
解答:解:(1)当λ≠0且λ≠-1时,直线l
1:
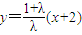
,直线l
2:y=
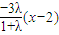
消参可得
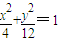
①
当λ=0时,直线l
1:x=-2,直线l
2:y=0,其交点为(-2,0),适合①;
当λ=-1时,直线l
1:y=0,直线l
2:x=2,其交点为(2,0),适合①;
∴点P的轨迹C的方程为
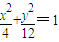
;
(2)假设存在直线l:y=kx+m(m≠0)与轨迹C相交于不同的两点M(x
1,y
1),N(x
2,y
2),且满足|BM|=|BN|.
令线段MN的中点M
(x
,y
),则BM
垂直平分MN
∵
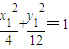
,
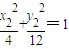
,
∴两式相减可得,
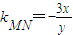
=k②
∵BM
⊥MN,∴

③
由②③可得
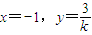
∴M
(-1,
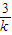
)
∵M
在椭圆C的内部,故

∴|k|>1
∵M
(-1,
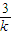
)在直线l上,
∴
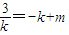
,
∴|m|=|k+
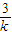
|≥
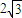
,当且仅当|k|=
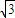
时取等号
∴存在直线l满足条件,此时m的取值范围为(-∞,-
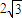
)∪(
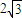
,+∞).
点评:本题考查轨迹方程,考查存在性问题的研究,考查学生分析解决问题的能力,属于中档题.

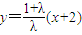 ,直线l2:y=
,直线l2:y=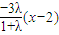
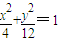 ①
①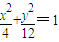 ;
;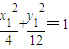 ,
,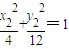 ,
,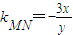 =k②
=k② ③
③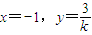
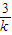 )
)
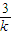 )在直线l上,
)在直线l上,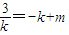 ,
,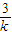 |≥
|≥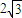 ,当且仅当|k|=
,当且仅当|k|=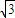 时取等号
时取等号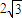 )∪(
)∪(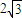 ,+∞).
,+∞).

 名校通行证有效作业系列答案
名校通行证有效作业系列答案