
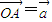 ,
, ,
, ,且
,且 ,
,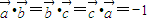 ,则
,则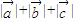 等于( )
等于( )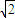
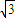
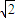
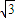
科目:高中数学 来源: 题型:
 3、如图,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是( )
3、如图,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是( )查看答案和解析>>
科目:高中数学 来源:2002年全国各省市高考模拟试题汇编 题型:013
有四个命题:
①若 是实数,则正整数n的最小值是4
是实数,则正整数n的最小值是4
②设z是虚数,则z+ ∈
∈
③若 都是非零复数,
都是非零复数,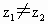 ,且复平面上O为原点,点A和B分别与
,且复平面上O为原点,点A和B分别与 和
和 对应,∠AOB=
对应,∠AOB= ,则
,则
④若复数z满足|z- |≤1,则
|≤1,则 ≤arg(-zi)≤
≤arg(-zi)≤ ,其中真命题是
,其中真命题是
[ ]
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
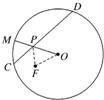 如图,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是
如图,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源:0113 期末题 题型:单选题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com