
科目:高中数学 来源:不详 题型:解答题
| 奖次 | 一等奖 | 二等奖 | 三等奖 |
| 随机数组的特征 | 3个1或3个0 | 只有2个1或2个0 | 只有1个1或1个0 |
| 资金(单位:元) | 5m | 2m | m |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 、
、 两盒中都有红球、白球,且球的形状、大小都相同,盒子
两盒中都有红球、白球,且球的形状、大小都相同,盒子 中有
中有 个红球与
个红球与 个白球,盒子
个白球,盒子 中有
中有 个红球与
个红球与 个白球(
个白球( ).
). 、
、 中各取一个球,
中各取一个球,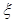 表示红球的个数;
表示红球的个数;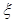 的分布列,并证明
的分布列,并证明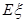 等于定值;
等于定值; 为何值时,
为何值时, 取到最小值,并求出最小值.
取到最小值,并求出最小值. 中不放回地摸取3个球,事件
中不放回地摸取3个球,事件 :在第一次取到红球后,以后两次都取到白球,事件
:在第一次取到红球后,以后两次都取到白球,事件 :在第一次取到白球后,以后两次都取到红球,若概率
:在第一次取到白球后,以后两次都取到红球,若概率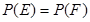 ,求
,求 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 排队人数 | 0 | 1 | 2 | 3 | 4 | 5人及5人以上 |
| 概率 | t | 0.3 | 0.16 | 0.3 | 0.1 | 0.04 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.p1p2 | B.p1(1-p2)+p2(1-p1) |
| C.1-p1p2 | D.1-(1-p1)(1-p2) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.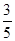 | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com