
【题目】已知函数f(x)=x﹣1+aex .
(1)若曲线y=f(x)在点(1,f(1))处的切线平行于x轴,求a的值;
(2)求f(x)的极值;
(3)当a=1时,曲线y=f(x)与直线y=kx﹣1没有公共点,求k的取值范围.
【答案】
(1)解:f(x)=x﹣1+aex.求导,f′(x)=1+aex.
由f′(1)=0,1+ae=0,解得:a=﹣ ![]() ,
,
∴a的值﹣ ![]()
(2)解:当a≥0,f′(x)>0恒成立,则f(x)在R上是增函数,无极值;
当a<0时,令f′(x)=0,则ex=﹣ ![]() ,x=ln(﹣
,x=ln(﹣ ![]() ),
),
x<ln(﹣ ![]() ),f′(x)>0;当x>ln(﹣
),f′(x)>0;当x>ln(﹣ ![]() ),f′(x)<0,
),f′(x)<0,
∴f(x)在(﹣∞,ln(﹣ ![]() ))上单调递增,在(ln(﹣
))上单调递增,在(ln(﹣ ![]() ),+∞)单调递减,
),+∞)单调递减,
f(x)在x=ln(﹣ ![]() )处取极大值,且极大值f(ln(﹣
)处取极大值,且极大值f(ln(﹣ ![]() ))=﹣ln(﹣a)﹣2,无极小值
))=﹣ln(﹣a)﹣2,无极小值
(3)解:当a=1时,f(x)=x﹣1+ex.
令g(x)=f(x)﹣(kx﹣1)=(1﹣k)x+ex,
由题意可知:g(x)=0无实数解,
假设k<1,此时g(0)=1>0,g( ![]() )=﹣1+
)=﹣1+ ![]() <0,
<0,
由函数g(x)的图象连续不断,由函数零点存在定理g(x)=0在R上至少有一解,
与方程g(x)=0,在R上没有实数解矛盾,故k≥1,
由k=1时,g(x)=ex,可知方程g(x)=0在R上没有实数解,
∴k的取值范围[1,+∞)
【解析】(1)求导,由题意可知f′(1)=0,即可求得a的值;(2)由(1)可知:分类讨论,根据导数与函数的单调性及极值的关系,即可求得f(x)的极值;(3)由题意可知g(x)=(1﹣k)x+ex=0无实数解,求导,根据函数的单调性及函数零点的判断,即可求得k的取值范围.
【考点精析】利用函数的极值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】已知{an}是各项为正数的等差数列,Sn为其前n项和,且4Sn=(an+1)2 . (Ⅰ)求a1 , a2的值及{an}的通项公式;
(Ⅱ)求数列 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工艺品厂要设计一个如图1所示的工艺品,现有某种型号的长方形材料如图2所示,其周长为4m,这种材料沿其对角线折叠后就出现图1的情况.如图,ABCD(AB>AD)为长方形的材料,沿AC折叠后AB'交DC于点P,设△ADP的面积为S2 , 折叠后重合部分△ACP的面积为S1 .
(Ⅰ)设AB=xm,用x表示图中DP的长度,并写出x的取值范围;
(Ⅱ)求面积S2最大时,应怎样设计材料的长和宽?
(Ⅲ)求面积(S1+2S2)最大时,应怎样设计材料的长和宽?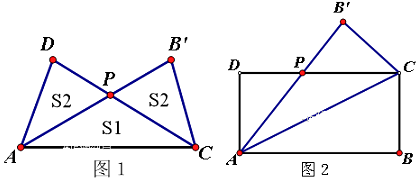
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 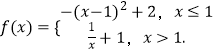 下列四个命题: ①f(f(1))>f(3);
下列四个命题: ①f(f(1))>f(3);
②x0∈(1,+∞), ![]() ;
;
③f(x)的极大值点为x=1;
④x1 , x2∈(0,+∞),|f(x1)﹣f(x2)|≤1
其中正确的有 . (写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (a>0). (Ⅰ)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(a>0). (Ⅰ)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若 ![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(Ⅲ)证明:总存在x0 , 使得当x∈(x0 , +∞),恒有f(x)<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( ) 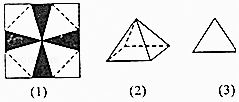
A.![]() cm3
cm3
B.![]() cm3
cm3
C.![]() cm3
cm3
D.![]() cm3
cm3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD为正三角形,其所在平面垂直于底面ABCD,若G为AD边的中点, 
(1)求证:BG⊥平面PAD;
(2)求证:AD⊥PB;
(3)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量 ![]() (m,n为实数),则m+n的取值范围是( )
(m,n为实数),则m+n的取值范围是( )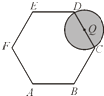
A.(1,2]
B.[5,6]
C.[2,5]
D.[3,5]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(log2x﹣2)(log4x﹣ ![]() )
)
(1)当x∈[2,4]时.求该函数的值域;
(2)若f(x)≥mlog2x对于x∈[4,16]恒成立,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com