
分析 若“p∨q”为真,“p∧q”为假,则p,q一真一假,进而可得实数m的取值范围.
解答 解:当P真时,?x∈R,x2+2x>m,
有△=4+4m<0,解得m<-1.…..(2分)
当q真时,?x0∈R,使${x_0}^2+2m{x_0}+2-m≤0$,
所以△=4m2-4(2-m)≥0,解得m≤-2,或m≥1 …..(4分)
又因为“p∨q”为真,“p∧q”为假,所以p,q一真一假,…..(6分)
当p真q假时,-2<m<-1…..(8分)
当p假q真时,m≥1…..(10分)
所以实数a的取值范围是(-2,-1)∪[1,+∞).…..(12分)
点评 本题以命题的真假判断与应用为载体,考查了复合命题,对数函数的图象和性质,不等式恒成立问题,难度中档.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
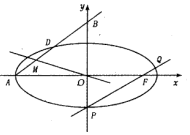 已知P(0,-1)是椭圆C的下顶点,F是椭圆C的右焦点,直线PF与椭圆C的另一个交点为Q,满足$\overrightarrow{PF}=7\overrightarrow{FQ}$.
已知P(0,-1)是椭圆C的下顶点,F是椭圆C的右焦点,直线PF与椭圆C的另一个交点为Q,满足$\overrightarrow{PF}=7\overrightarrow{FQ}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 科目选择 | 物理 化学 生物 | 历史 地理 政治 | 物理 化学 地理 | 历史 地理 生物 | 物理 政治 历史 | 其他 |
| 频率 | $\frac{1}{5}$ | $\frac{1}{6}$ | $\frac{2}{15}$ | a | b | c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x<3} | B. | {-1,0,1} | C. | {x|-1<x<2} | D. | {0,1,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com