
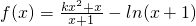 .
.
 ,
, …(2分)
…(2分) ,
, …(5分)
…(5分) =
= …(7分)
…(7分) …(8分)
…(8分) ,解得
,解得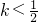 ,令
,令  ,解得k<1…(10分)
,解得k<1…(10分)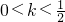 时,
时, ,
, 上减,在区间
上减,在区间 上增,…(11分)
上增,…(11分) 时,f'(x)≥0,此时f(x)在区间(-1,+∞)上增,…(12分)
时,f'(x)≥0,此时f(x)在区间(-1,+∞)上增,…(12分)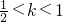 时,
时, ,
, 上增,
上增, 上减,在区间(0,+∞)上增,…(13分)
上减,在区间(0,+∞)上增,…(13分) ,
,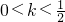 ,k=
,k= ,
, <k<1,k>1四种情形,在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0即可.
<k<1,k>1四种情形,在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0即可.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
| 1 | f(x)+m |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 2c+t |
| c+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| kx-(k+1) | x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 2 |
| 2x-x2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com