
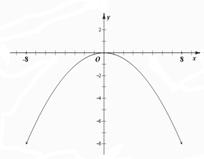
本题10分)如图,河道上有一座抛物线型拱桥,在正常水位时,拱圈最高点距水面为8m,拱圈内水面宽16 m., 为保证安全,要求通过的船顶部(设为平顶)与拱桥顶部在竖直方向上高度之差至少要有0.5m.
(1)一条船船顶部宽4m,要使这艘船安全通过,则船在水面以上部分高不能超过多少米?
(2)近日因受台风影响水位暴涨2.7m,为此必须加重船载,降低船身,才能通过桥洞. 试问:一艘顶部宽 m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?
m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?

(1)如图所示,以过拱桥的最高点且平行水面的直线为X轴,最高点O为原点建立直角坐标系 ------------------------------------------- 1分
设抛物线方程为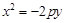 ,将点
,将点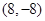 代入得
代入得 =8,
=8, 抛物线方程是
抛物线方程是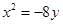 ,-------------------------------------------4分
,-------------------------------------------4分
 将
将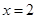 代入得
代入得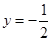 ,
, , 故船在水面以上部分高不能超过7米。-------------------------------------------
6分
, 故船在水面以上部分高不能超过7米。-------------------------------------------
6分
(2)将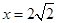 代入方程
代入方程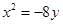 得
得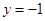 ,-------------------------------------------
8分
,-------------------------------------------
8分
此时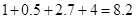 ,故船身应至少降低
,故船身应至少降低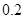 米-------------------------------------10分
米-------------------------------------10分
【解析】略


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源:2013届陕西西安音乐学院附属中等音乐学校高二下期末数学试卷(解析版 题型:解答题
(本题10分)如图一边长为48cm的正方形铁皮,四角各截去一个大小相同的小正方形,然后折起,可以做成一个无盖长方体容器。所得容器的体积V(单位: )是关于截去的小正方形的边长x(单位:
)是关于截去的小正方形的边长x(单位: )的函数。⑴ 随着x的变化,容积V是如何变化的?
)的函数。⑴ 随着x的变化,容积V是如何变化的?
⑵ 截去的小正方形的边长为多少时,容器的容积最大?最大容积是多少?












查看答案和解析>>
科目:高中数学 来源:2011-2012年山东省济宁市高二上学期期中考试文科数学 题型:解答题
(本题10分)如图,已知点A(2,3), B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上
(Ⅰ)求AB边上的高CE所在直线的方程
(Ⅱ)求△ABC的面积
查看答案和解析>>
科目:高中数学 来源:2012届辽宁省抚顺市六校联合体高二下学期期末考试数学 题型:解答题
请考生在(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分。
(本题10分)
 如图,
如图, 内接于⊙O,过点A的直线交⊙O于点P,交BC的延长线于点D,且
内接于⊙O,过点A的直线交⊙O于点P,交BC的延长线于点D,且
(Ⅰ)求证: 
(Ⅱ)如果 ,⊙O的半径为1,
,⊙O的半径为1,
且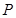 为弧
为弧 的中点,求
的中点,求 的长。
的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com