
科目:高中数学 来源:2016届云南省高三适应性月考八理科数学试卷(解析版) 题型:解答题
国内某大学有男生6000人,女生4000人,该校想了解本校学生的运动状况,根据性别采取分层抽样的方法从全校学生中抽取100人,调查他们平均每天运动的时间(单位:小时),统计表明该校学生平均每天运动的时间范围是 ,若规定平均每天运动的时间不少于2小时的学生为“运动达人”,低于2小时的学生为“非运动达人”. 根据调查的数据按性别与“是否为‘运动达人’” 进行统计,得到如下
,若规定平均每天运动的时间不少于2小时的学生为“运动达人”,低于2小时的学生为“非运动达人”. 根据调查的数据按性别与“是否为‘运动达人’” 进行统计,得到如下 列联表:
列联表:
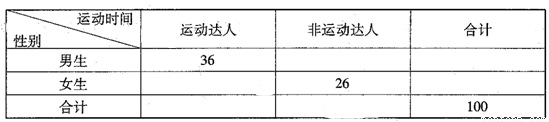
(1)请根据题目信息,将 列联表中的数据补充完整,并通过计算判断能否在犯错误概率不超过0.025的前提下认为性别与“是否为‘运动达人’”有关;
列联表中的数据补充完整,并通过计算判断能否在犯错误概率不超过0.025的前提下认为性别与“是否为‘运动达人’”有关;
(2)将此样本的频率估计为总体的概率,随机调查该校的3名男生,设调查的3人中运动达人的人数为随机变量 ,求
,求 的分布列和数学期望
的分布列和数学期望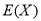 及方差
及方差 .
.

查看答案和解析>>
科目:高中数学 来源:2016届西藏日喀则一中高三下学期二模理科数学试卷(解析版) 题型:解答题
已知正项数列 的前
的前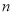 项和为
项和为 ,且
,且 ,数列
,数列 满足
满足 ,且
,且 .
.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)记 ,求
,求 .
.
查看答案和解析>>
科目:高中数学 来源:2016届江苏省高三考前一周双练三模数学试卷(解析版) 题型:解答题
设 且
且 ,集合
,集合 的所有
的所有 个元素的子集记为
个元素的子集记为 ,
, ,
, ,
, .
.
(1)求集合 ,
, ,
, ,
, 中所有元素之和
中所有元素之和 ;
;
(2)记 为
为 (
( ,
, ,
, ,
, )中最小元素与最大元素之和,求
)中最小元素与最大元素之和,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2016届江苏省高三考前一周双练三模数学试卷(解析版) 题型:解答题
对于数列 ,若从第二项起,每一项与它前一项的差依次组成等比数列,则称该等比数列为“差等比数列”,现已知
,若从第二项起,每一项与它前一项的差依次组成等比数列,则称该等比数列为“差等比数列”,现已知 ,设其差等比数列的首项为
,设其差等比数列的首项为 ,公比为
,公比为 (
( ).
).
(1)是否存在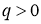 ,使得数列
,使得数列 是等差数列或等比数列?若存在,求出
是等差数列或等比数列?若存在,求出 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(2)当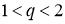 时,若
时,若 是公差为
是公差为 的等差数列,且
的等差数列,且 .试确定
.试确定 的取值范围,使得
的取值范围,使得 .
.
查看答案和解析>>
科目:高中数学 来源:2016届江苏省高三考前一周双练三模数学试卷(解析版) 题型:填空题
如图甲所示,在直角 中,
中, 、
、 ,
, 是垂足,则有
是垂足,则有 ,该结论称为射影定理.如图乙所示,在三棱锥
,该结论称为射影定理.如图乙所示,在三棱锥 中,
中, 平面
平面 ,
, 平面
平面 ,
, 为垂足,且
为垂足,且 在
在 内,类比直角三角形中的射影定理,则有 .
内,类比直角三角形中的射影定理,则有 .

查看答案和解析>>
科目:高中数学 来源:2016届山西省高考考前质量检测三理科数学试卷(解析版) 题型:选择题
在体积为 的三棱锥
的三棱锥 中,
中, ,且平面
,且平面 平面
平面 ,若该三棱锥的四个顶点都在同一球面上,则该球的体积是( )
,若该三棱锥的四个顶点都在同一球面上,则该球的体积是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com