
【题目】给定椭圆C: ![]() +
+ ![]() =1(a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为
=1(a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为 ![]() ,且经过点(0,1).
,且经过点(0,1).
(1)求实数a,b的值;
(2)若过点P(0,m)(m>0)的直线l与椭圆C有且只有一个公共点,且l被椭圆C的伴随圆C1所截得的弦长为2 ![]() ,求实数m的值.
,求实数m的值.
【答案】
(1)解:记椭圆C的半焦距为c.
由题意,得b=1, ![]() =
= ![]() ,c2=a2+b2,
,c2=a2+b2,
解得a=2,b=1.
(2)解:由(1)知,椭圆C的方程为 ![]() +y2=1,圆C1的方程为x2+y2=5.
+y2=1,圆C1的方程为x2+y2=5.
显然直线l的斜率存在.
设直线l的方程为y=kx+m,即kx﹣y+m=0.
因为直线l与椭圆C有且只有一个公共点,
故方程组 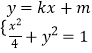 (*)有且只有一组解.
(*)有且只有一组解.
由(*)得(1+4k2)x2+8kmx+4m2﹣4=0.
从而△=(8km)2﹣4(1+4k2)( 4m2﹣4)=0.
化简,得m2=1+4k2.①…(10分)
因为直线l被圆x2+y2=5所截得的弦长为2 ![]() ,
,
所以圆心到直线l的距离d= ![]() =
= ![]() .
.
即 ![]() =
= ![]() . ②
. ②
由①②,解得k2=2,m2=9.
因为m>0,所以m=3.
【解析】(1)记椭圆C的半焦距为c.由题意,得b=1, ![]() =
= ![]() ,由此能求出a,b.(2)由(1)知,椭圆C的方程为
,由此能求出a,b.(2)由(1)知,椭圆C的方程为 ![]() +y2=1,圆C1的方程为x2+y2=5.设直线l的方程为y=kx+m,由
+y2=1,圆C1的方程为x2+y2=5.设直线l的方程为y=kx+m,由 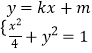 ,得(1+4k2)x2+8kmx+4m2﹣4=0.由此利用根的判别式、弦长公式、圆心到直线的距离,结合知识点能求出m.
,得(1+4k2)x2+8kmx+4m2﹣4=0.由此利用根的判别式、弦长公式、圆心到直线的距离,结合知识点能求出m.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图. 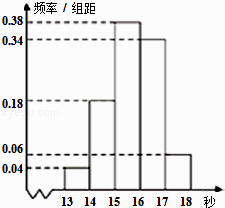
(1)若成绩在区间[14,16)内规定为良好,求该班在这次百米测试中成绩为良好的人数;
(2)请根据频率分布直方图估计样本数据的众数和中位数(精确到0.01).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合M={x|﹣a<x<a+1,a∈R},集合N={x|x2﹣2x﹣3≤0}.
(1)当a=1时,求M∪N及N∩RM;
(2)若x∈M是x∈N的充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校随机抽取某次高三数学模拟考试甲、乙两班各10名同学的客观题成绩(满分60分),统计后获得成绩数据的茎叶图(以十位数字为茎,个位数字为叶),如图所示: (Ⅰ)分别计算两组数据的平均数,并比较哪个班级的客观题平均成绩更好;
(Ⅱ)从这两组数据各取两个数据,求其中至少有2个满分(60分)的概率;
(Ⅲ)规定客观题成绩不低于55分为“优秀客观卷”,以这20人的样本数据来估计此次高三数学模拟的总体数据,若从总体中任选4人,记X表示抽到“优秀客观卷”的学生人数,求X的分布列及数学期望.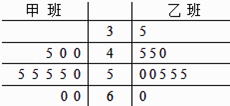
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在半径为40cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中A,B在直径上,点C,D在圆周上、 
(1)设AD=x,将矩形ABCD的面积y表示成x的函数,并写出其定义域;
(2)怎样截取,才能使矩形材料ABCD的面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两名同学在某项测试中得分成绩的茎叶图如图所示,x1 , x2分别表示知甲、乙两名同学这项测试成绩的众数,s12 , s22分别表示知甲、乙两名同学这项测试成绩的方差,则有( ) 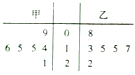
A.x1>x2 , s12<s22
B.x1=x2 , s12>s22
C.x1=x2 , s12=s22
D.x1=x2 , s12<s22
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com