
如图所示,已知圆O外有一点P,作圆O的切线PM,M为切点,过PM的中点N,作割线NAB,交圆于A、B两点,连接PA并延长,交圆O于点C,连接PB交圆O于点D,若MC=BC.

(1)求证:△APM∽△ABP;
(2)求证:四边形PMCD是平行四边形.
见解析
【解析】
证明:(1)∵PM是圆O的切线,NAB是圆O的割线,N是PM的中点,
∴MN2=PN2=NA·NB,
∴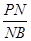 =
=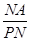 ,
,
又∵∠PNA=∠BNP, ∴△PNA∽△BNP,
∴∠APN=∠PBN, 即∠APM=∠PBA.
∵MC=BC, ∴∠MAC=∠BAC,
∴∠MAP=∠PAB,
∴△APM∽△ABP.
(2)∵∠ACD=∠PBN,
∴∠ACD=∠PBN=∠APN,即∠PCD=∠CPM,
∴PM∥CD,
∵△APM∽△ABP,∴∠PMA=∠BPA,
∵PM是圆O的切线,∴∠PMA=∠MCP,
∴∠PMA=∠BPA=∠MCP,即∠MCP=∠DPC,
∴MC∥PD,
∴四边形PMCD是平行四边形.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•肇庆一模)(几何证明选讲选做题)
(2013•肇庆一模)(几何证明选讲选做题)| 3 |
| 15 |
查看答案和解析>>
科目:高中数学 来源:2010-2011年海南省高一下学期质量检测数学试卷(一)B卷 题型:解答题
、已知圆O:x2+y2=13
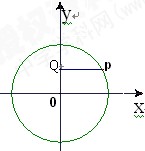
(1)证明:点A(-1,5)在圆O外。
(2)如图所示,经过圆O上任P一点作y轴的垂线,垂足为Q,求线段PQ的中点M的轨迹方程。(12分)
查看答案和解析>>
科目:高中数学 来源:2013年广东省肇庆市高考数学一模试卷(理科)(解析版) 题型:填空题
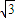 ,
,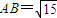 ,则AC的长为 .
,则AC的长为 .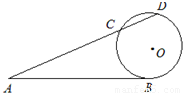
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com