
 如图,现有一块矩形空地,要在这块空地上开辟一个内
如图,现有一块矩形空地,要在这块空地上开辟一个内 接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知
接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知 ,
,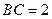 ,且
,且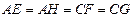 ,设
,设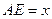 ,绿地面积为
,绿地面积为 .
. 关于
关于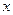 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域; 为何值时,绿地面积
为何值时,绿地面积 最大?
最大?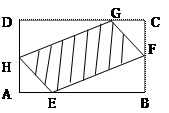
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
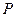 的关系近似地满足
的关系近似地满足 :
: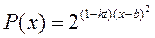 (其中
(其中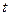 为关税的税率,且
为关税的税率,且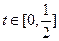 ,
,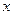 为市场价格,
为市场价格,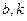 为正常数),当
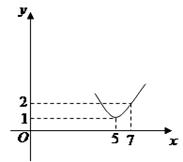
为正常数),当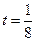 时的市场供应量曲线如图所示;
时的市场供应量曲线如图所示;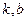 的值;
的值;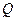 ,它近似满足
,它近似满足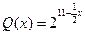 .
. 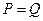 时的市场价格称为均衡价格,为使均衡价格控制在不低于9元的范围内,求税率
时的市场价格称为均衡价格,为使均衡价格控制在不低于9元的范围内,求税率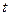 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 消费金额(元)的范围 | [200,400) | [400,500) | [500,700) | [700,900 ) | … |
| 获得奖券的金额(元) | 30 | 60 | 100 | 130 | … |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
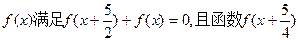 为奇函数.
为奇函数. 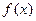 的最小正周期是
的最小正周期是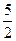 ;②函数
;②函数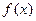 的图象关于点(
的图象关于点(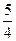 ,0)
,0)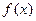 的图象关于直线
的图象关于直线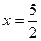 对称;④函数
对称;④函数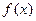 的最大值为
的最大值为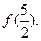

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com