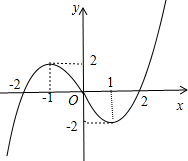
(本小题满分12分)
解:(Ⅰ)如图所示. …(4分)
(Ⅱ)任取x∈(-∞,0),则-x∈(0,+∞)
由f(x)为奇函数,
则f(x)=-f(-x)=-[2(-x)
2-4(-x)]=-2x
2-4x…(6分)
综上所述,
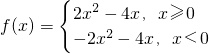
…(7分)
评分建议:
用待定系数法也可以完成,参照以上评分标准给分;
观察图象,直接得出函数解析式,没有中间过程,建议这次不扣分;
如果最后结果不写成分段形式,应当扣(1分).
(Ⅲ)任取x
1,x
2∈[1,+∞),且x
1<x
2,…(8分)
则f(x
1)-f(x
2)=
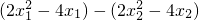
…(9分)
=
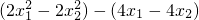
=2(x
1+x
2)(x
1-x
2)-4(x
1-x
2)
=2(x
1-x
2)[(x
1+x
2)-2]…(10分)
∵x
1<x
2∴x
1-x
2<0
又由x
1,x
2∈[1,+∞),且x
1<x
2,所以x
1+x
2>2,∴(x
1+x
2)-2>0
∴2(x
1-x
2)[(x
1+x
2)-2]<0,
∴f(x
1)-f(x
2)<0,即f(x
1)<f(x
2)…(11分)
∴函数f(x)=2x
2-4x在区间[1,+∞)上单调递增.…(12分)
评分建议:如果不强调取值的任意性,建议酌情扣(1分).
分析:(1)根据奇函数的图象关于原点对称这一性质即可补全函数f(x)的图象.
(Ⅱ)任取x∈(-∞,0),则-x∈(0,+∞)f(-x)=2(-x)
2-4(-x)=2x
2+4x再根据f(x)为奇函数即满足f(x)=-f(-x)即可求出f(x)在x∈(-∞,0)的解析式从而即可求出函数f(x)的表达式.
(Ⅲ)直接根据单调递增函数的定义证明即可.
点评:本题主要考察了奇函数的定义和性质以及利用定义法证明单调函数,属中档题,较难.解题的关键是透彻理解奇函数的图象关于原点对称且有f(x)=-f(-x)这是求解f(x)的表达式的关键所在并且结果要写成分段函数的形式而对于利用定义法证明单调函数要抓住作差--变形--定号--下结论这四步即可!

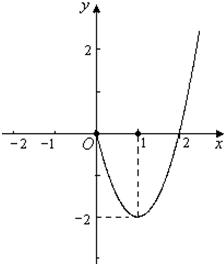 若函数f(x)为奇函数,当x≥0时,f(x)=2x2-4x(如图).
若函数f(x)为奇函数,当x≥0时,f(x)=2x2-4x(如图).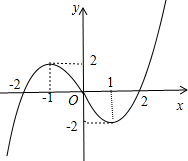 (本小题满分12分)
(本小题满分12分)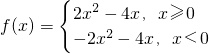 …(7分)
…(7分)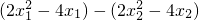 …(9分)
…(9分)


 智能训练练测考系列答案
智能训练练测考系列答案