Question

在△ABC中,a、b、c分别是角A、B、C的对边,S是该三角形的面积,且4sin(3π-A)sin²(+)-cos(π-2A)=+1.

(1)求角A的大小;

(2)若角A为锐角,b=1,S=,求边BC上的中线AD的长

Answer 1

解:(1)原式4sinAsin²(+)+cos2A=3+1

4sinA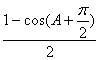+1-2sin²A=+12sinA(1+sinA)-2sin²A=sinA=.

因为A∈(0,π),则A=或.

(2)因为A为锐角,则A=,即cosA=.而面积S=bcsinA,

又S=,b=1,sinA=,则c=4.

方法一:又由余弦定理a²=b²+c²-2bccosA,得a=,

又cosC==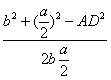,得=,

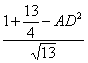即AD=.

方法二:作CE平行于AB,并延长AD交CE于点E,在△ACE中,∠C=,AC=1,CE=4,且AD=AE,又AE²=AC²+CE²-2AC·CE·cosC,

即AE²=1+16+8×=21.这样AD=AE=.