
已知函数

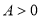 ,
,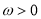 ,
,

在一个周期内,当 时,
时,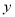 有最大值为
有最大值为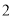 ,当
,当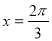 时,
时, 有最小值为
有最小值为 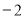 .
.
(1)求函数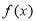 表达式;(2)若
表达式;(2)若 ,求
,求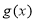 的单调递减区间.
的单调递减区间.
科目:高中数学 来源:2016届山东省济宁市高一5月质量检测数学试卷(解析版) 题型:选择题
已知函数 的最小正周期为
的最小正周期为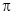 ,则该函数的图象( )
,则该函数的图象( )
A.关于点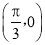 对称 B.关于直线
对称 B.关于直线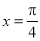 对称
对称
C.关于点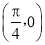 对称 D.关于直线
对称 D.关于直线 对称
对称
查看答案和解析>>
科目:高中数学 来源:2016届山东省高一下学期期中检测数学试卷(解析版) 题型:选择题
为了得到函数y=cos(x+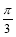 )的图象,只需把余弦曲线y=cosx上的所有的点 ( )
)的图象,只需把余弦曲线y=cosx上的所有的点 ( )
A.向左平移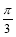 个单位长度 B.向右平移
个单位长度 B.向右平移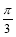 个单位长度
个单位长度
C.向左平移 个单位长度 D.向右平移
个单位长度 D.向右平移 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源:2016届山东省高一下学期期末模拟检测一数学试卷(解析版) 题型:填空题
已知下列命题:①函数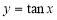 在第一象限是增函数;
在第一象限是增函数;
②函数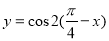 是偶函数; ③函数
是偶函数; ③函数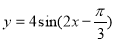 的一个对称中心是(
的一个对称中心是(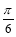 ,0);
,0);
④函数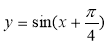 在闭区间
在闭区间 上是增函数;
上是增函数;
写出所有正确的命题的题号: .
查看答案和解析>>
科目:高中数学 来源:2016届山东省德州市高一下学期期末考试数学试卷(解析版) 题型:填空题
12.某企业有3个分厂生产同一种电子产品,第一、二、三分厂的产量之比为1:2:1,用分层抽样方法(每个分厂的产品为一层)从3个分厂生产的电子产品中共抽取100件作使用寿命的测试,由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均值分别为980h,1020h,1032h,则抽取的100件产品的使用寿命的平均值为 _________ h.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com