
(本小题满分l 2分)某书商为提高某套丛书的销量,准备举办一场展销会.据市场调查,当每套丛书售价定为x元时,销售量可达到15一O.1x万套.现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为l0.假设不计其它成本,即销售每套丛书的利润 = 售价 一 供货价格.问:
(I)每套丛书定价为100元时,书商能获得的总利润是多少万元?
(Ⅱ)每套丛书定价为多少元时,单套丛书的利润最大?
解:(Ⅰ)每套丛书定价为100元时,销售量为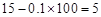 万套,
万套,
此时每套供货价格为 元,················· 3分
元,················· 3分
∴ 书商所获得的总利润为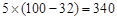 万元.·········· 4分
万元.·········· 4分
(Ⅱ)每套丛书售价定为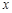 元时,由
元时,由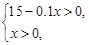 得,
得,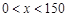 ,··· 5分
,··· 5分
依题意,单套丛书利润
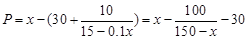 ·············· 7分
·············· 7分
∴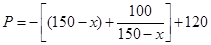 ,
,
∵ 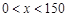 ,∴
,∴ 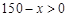 ,
,
由 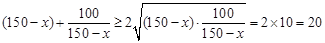 ,
······· 10分
,
······· 10分
当且仅当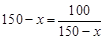 ,即
,即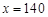 时等号成立,此时
时等号成立,此时
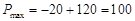 .
.
答:(Ⅰ)当每套丛书售价定为100元时,书商能获得总利润为340万元;(Ⅱ)每套丛书售价定为140元时,单套利润取得最大值100元.·························· 12分
(说明:学生未求出最大值不扣分).
【解析】略


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 5 |
| π |
| 4 |
| a |
| b |
| c |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省福州市高三质量检测理科数学 题型:解答题
(本小题满分1 3分)
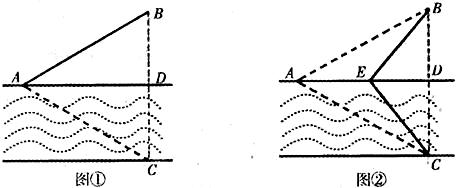
如图①,一条宽为l km的两平行河岸有村庄A和供电站C,村庄B与A、C的直线距离都是2km,BC与河岸垂直,垂足为D.现要修建电缆,从供电站C向村庄A、B供电.修建地下电缆、水下电缆的费用分别是2万元/km、4万元/km.
(Ⅰ)已知村庄A与B原来铺设有旧电缆仰,需要改造,旧电缆的改造费用是0.5万元/km.现
决定利用旧电缆修建供电线路,并要求水下电缆长度最短,试求该方案总施工费用的最小值.
(Ⅱ)如图②,点E在线段AD上,且铺设电缆的线路为CE、EA、EB.若∠DCE=θ (0≤θ≤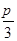 ),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省福州市高三第一学期期末质量检测理科数学 题型:解答题
(本小题满分l 3分)在数列{an}中,a1=2,an+l=an+cn (n∈N*,常数c≠0),且a1,a2,a3成等比数列.
(I)求c的值;
(Ⅱ)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省福州市高三第一学期期末质量检测文科数学 题型:解答题
.(本小题满分l 2分) 已知{an}是等比数列,a1=2,且a1,a3+1,a4成等差数列.
(I)求数列{a n}的通项公式;
(Ⅱ)若bn=log2 an,求数列{bn}的前n项和Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com