
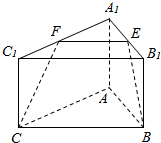
 如图所示,三棱柱ABC-A1B1C1中,E,F分别是A1B1,A1C1的中点.截面BCFE将三棱柱分成两部分,你能说出多面体A1EF-ABC是什么样的几何体吗?多面体B1C1FE-BC是简单几何体还是组合体?为什么?
如图所示,三棱柱ABC-A1B1C1中,E,F分别是A1B1,A1C1的中点.截面BCFE将三棱柱分成两部分,你能说出多面体A1EF-ABC是什么样的几何体吗?多面体B1C1FE-BC是简单几何体还是组合体?为什么? 分析 根据几何体的结构特征得出多面体A1EF-ABC是三棱台,多面体B1C1FE-BC是组合体,分别说明即可.
解答 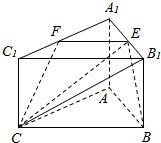 解:截面BCFE将三棱柱分成两部分,多面体A1EF-ABC是三棱台,
解:截面BCFE将三棱柱分成两部分,多面体A1EF-ABC是三棱台,
多面体B1C1FE-BC是组合体;
因为:E,F分别是A1B1,A1C1的中点,所以$\frac{{A}_{1}F}{AC}$=$\frac{{A}_{1}E}{AB}$=$\frac{EF}{BC}$=$\frac{1}{2}$,
所以AA1,BE和CF的延长线交于一点.组成棱锥,
所以多面体A1EF-ABC是三棱台;
又连接CE和CB1,得出多面体B1C1FE-BC是:
四棱锥C-B1C1FE和三棱锥C-BEB1的组合体,如图所示.
点评 本题考查了判断空间几何体结构特征的应用问题,是基础题目.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | 奇函数,在区间(1,+∞)上是减函数 | B. | 奇函数,在区间(1,+∞)上是增函数 | ||
| C. | 偶函数,在区间(0,1)上是增函数 | D. | 偶函数,在区间(0,1)上是减函数. |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com