
分析 由已知结合向量共线可得(a2+b2)sin(A-B)-(a2-b2)sin(A+B)=0,展开两角和与差的正弦,再利用正弦定理化边为角,可得sin2B=sin2A,再由c=120°,可得A=B=30°.
解答 解:由$\overrightarrow{m}$=(sin(A-B),a2-b2)与$\overrightarrow{n}$=(sin(A+B),a2+b2)共线,
可得(a2+b2)sin(A-B)-(a2-b2)sin(A+B)=0,
即(a2+b2)(sinAcosB-cosAsinB)-(a2-b2)(sinAcosB+cosAsinB)=0.
整理得:b2sinAcosB-a2cosAsinB=0,
由$\frac{a}{sinA}=\frac{b}{sinB}=2R$,代入上式得sin2BsinAcosB-sin2AcosAsinB=0,
∵A,B为三角形的内角,∴sinA•sinB≠0,得
sinBcosB-sinAcosA=0,即sin2B=sin2A,
∵c=120°,∴A=B=30°.
故答案为:30°.
点评 本题考查平面向量的数量积运算,考查了正弦定理在解三角形中的应用,是中档题.


科目:高中数学 来源: 题型:解答题
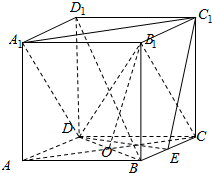 已知正方体ABCD-A1B1C1D1,底面ABCD的中心为O,E为BC的中点,如图
已知正方体ABCD-A1B1C1D1,底面ABCD的中心为O,E为BC的中点,如图查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
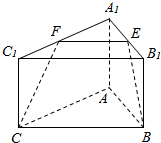 如图所示,三棱柱ABC-A1B1C1中,E,F分别是A1B1,A1C1的中点.截面BCFE将三棱柱分成两部分,你能说出多面体A1EF-ABC是什么样的几何体吗?多面体B1C1FE-BC是简单几何体还是组合体?为什么?
如图所示,三棱柱ABC-A1B1C1中,E,F分别是A1B1,A1C1的中点.截面BCFE将三棱柱分成两部分,你能说出多面体A1EF-ABC是什么样的几何体吗?多面体B1C1FE-BC是简单几何体还是组合体?为什么?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com