
如图,在正方形 中,
中, 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,分别将线段
,分别将线段 和
和 十等分,分点分别记为
十等分,分点分别记为 和
和 ,连接
,连接 ,过
,过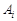 作
作 轴的垂线与
轴的垂线与 交于点
交于点 。
。

(Ⅰ)求证:点 都在同一条抛物线上,并求抛物线
都在同一条抛物线上,并求抛物线 的方程;
的方程;
(Ⅱ)过点 作直线
作直线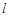 与抛物线E交于不同的两点
与抛物线E交于不同的两点 , 若
, 若 与
与 的面积之比为4:1,求直线
的面积之比为4:1,求直线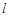 的方程。
的方程。
(Ⅰ)见解析(Ⅱ)直线 的方程为
的方程为 ,即
,即 或
或
【解析】(Ⅰ)依题意,过 且与x轴垂直的直线方程为
且与x轴垂直的直线方程为
 ,
, 直线
直线 的方程为
的方程为
设 坐标为
坐标为 ,由
,由 得:
得: ,即
,即 ,
,

 都在同一条抛物线上,且抛物线
都在同一条抛物线上,且抛物线 方程为
方程为
(Ⅱ)依题意:直线 的斜率存在,设直线
的斜率存在,设直线 的方程为
的方程为
由 得
得
此时 ,直线
,直线 与抛物线
与抛物线 恒有两个不同的交点
恒有两个不同的交点
设: ,则
,则



又 ,
,

分别带入 ,解得
,解得
直线 的方程为
的方程为 ,即
,即 或
或
此题在问法上给学生设了一个卡,如果第一问直接问 的轨迹方程,估计学生更容易入手一些,不过对于知识要活学活用(证明它求出不就说明问题了)。那么第二问有关解析几何的计算就要善于转化,且计算要过关。
的轨迹方程,估计学生更容易入手一些,不过对于知识要活学活用(证明它求出不就说明问题了)。那么第二问有关解析几何的计算就要善于转化,且计算要过关。
【考点定位】 本题考查抛物线的性质、直线与抛物线的位置关系等基础知识,考查运算求解能力,化归与转化及数形结合思想、函数与方程思想。属于中等难度。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2010-2011学年江苏省苏、锡、常、镇四市高三调研测试数学卷(一) 题型:填空题
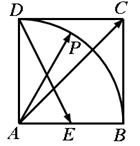
如图,在正方形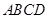 中,
中,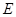 为
为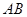 的中点,
的中点,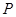 为以
为以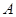 为圆心、
为圆心、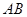 为半径的圆弧上的任意一点,设向量
为半径的圆弧上的任意一点,设向量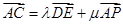 ,则
,则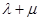 的最小值为
;
的最小值为
;
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在正方形![]() 中,
中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .分别将线段
.分别将线段![]() 和
和![]() 十等分,分点分别记为
十等分,分点分别记为![]() 和
和![]() ,连结
,连结![]() ,过
,过![]() 做
做![]() 轴的垂线与
轴的垂线与![]() 交于点
交于点![]() .
.
(1)求证:点![]() 都在同一条抛物线上,并求该抛物线
都在同一条抛物线上,并求该抛物线![]() 的方程;
的方程;
(2)过点![]() 做直线
做直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,若
,若![]() 与
与![]() 的面积比为
的面积比为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源:2011届江苏省苏、锡、常、镇四市高三调研测试数学卷(一) 题型:填空题
如图,在正方形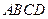 中,
中,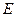 为
为 的中点,
的中点,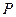 为以
为以 为圆心、
为圆心、 为半径的圆弧上的任意一点,设向量
为半径的圆弧上的任意一点,设向量 ,则
,则 的最小值为 ;
的最小值为 ;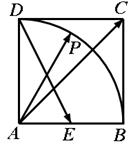
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com