
����Ŀ��ij����Ʒ��Ҫ������ͼ��ʾ��һ�ֹ���Ʒ���ù���Ʒ��һ��ʵ��Բ�����һ��ʵ����������ɣ�Ҫ�����İ뾶��Բ���ĵ���뾶֮��Ϊ![]() ������Ʒ�����Ϊ
������Ʒ�����Ϊ![]() ������Բ���ĵ���뾶Ϊ
������Բ���ĵ���뾶Ϊ![]() ������Ʒ�ı����Ϊ
������Ʒ�ı����Ϊ![]() ��������Բ���ĽӴ�������Բ��ơ�
��������Բ���ĽӴ�������Բ��ơ�

��1�����![]() ����
����![]() �ĺ�����ϵʽ�����
�ĺ�����ϵʽ�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��������Ʋ���ʹ����Ʒ�ı������С���������Сֵ��
�ο���ʽ���������ʽ��![]() ����������ʽ��
����������ʽ��![]() ������
������![]() Ϊ��뾶.
Ϊ��뾶.
���𰸡���1��![]() ����2������Բ���ĸ�Ϊ
����2������Բ���ĸ�Ϊ![]() ��Բ���ĵ���뾶Ϊ
��Բ���ĵ���뾶Ϊ![]() ������İ뾶Ϊ
������İ뾶Ϊ![]() ��ƣ�����Ʒ�ı������С��Ϊ
��ƣ�����Ʒ�ı������С��Ϊ![]() .
.
��������
��1������֪��Բ���ĵ���뾶Ϊ2x������İ뾶Ϊ3x����Բ���ĸ�Ϊh��ͨ������Ʒ����������Բ���ĸ������뾶�Ĺ�ϵ��Ȼ��д��S����x�ĺ�����ϵʽ��
��2�����ã�1���ı���ʽ��ͨ�������������ֵ�㣬˵���ߡ�����뾶����İ뾶����ֵʹ����Ʒ�ı������С��
��1������֪��Բ���ĵ���뾶Ϊ![]() ������İ뾶Ϊ
������İ뾶Ϊ![]() ����Բ���ĸ�Ϊ
����Բ���ĸ�Ϊ![]() ��
��
�߹���Ʒ�����Ϊ![]() ����
����![]() ����
����![]() ��
��
���Ʒ�ı����Ϊ![]()
![]() ��
��
��![]() ����
����![]() ����
����![]() ��
��
��![]() ��
��
��2���ɣ�1��֪��![]() ��
��
��![]() ����
����![]() �����
�����
|
| 1 |
|
|
| 0 | + |
| �K |
| �J |
��![]() ��
��![]() �ݼ�����
�ݼ�����![]() ����.
����.
��![]() ����ʱ
����ʱ![]() ��
��
�𣺰���Բ���ĸ�Ϊ![]() ��Բ���ĵ���뾶Ϊ
��Բ���ĵ���뾶Ϊ![]() ������İ뾶Ϊ
������İ뾶Ϊ![]() ��ƣ�����Ʒ�ı������С��Ϊ
��ƣ�����Ʒ�ı������С��Ϊ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ����x�ʣ���3��2��ʱ��
����x�ʣ���3��2��ʱ��![]() >0����x�ʣ���
>0����x�ʣ���![]() ����3��
����3��![]() ��2��+
��2��+![]() ��ʱ��
��ʱ��![]() <0
<0
��I����a��b��ֵ��
��II��������ʽ![]() �Ľ⼯ΪR����ʵ��c��ȡֵ��Χ.
�Ľ⼯ΪR����ʵ��c��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����n��4������M={1��2��3������n}�����к���4��Ԫ�ص��Ӽ���ΪA1 �� A2 �� A3 �� ���� ![]() ��
��
��A1 �� A2 �� A3 �� ���� ![]() ������Ԫ��֮��ΪSn ��
������Ԫ��֮��ΪSn ��
��1����S4 �� S5 �� S6�����Sn��
��2��֤����S4+S5+��+Sn=10Cn+26 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ ![]() ��
�� ![]() �Ƿ��㲻���ߵ���������
�Ƿ��㲻���ߵ��������� ![]() =
= ![]()
![]() +
+ ![]()
![]() ������㼯M={K|
������㼯M={K| ![]() =
= ![]() }����K1 �� K2��Mʱ�������������r��2������ʽ|
}����K1 �� K2��Mʱ�������������r��2������ʽ| ![]() |��c|
|��c| ![]() |���������ʵ��c����СֵΪ ��
|���������ʵ��c����СֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ҹ��Ŵ�����ѧ���������ݼ�Ϊ�ḻ���������������⣺���������˷���Ǯ�����϶��������������˵ȣ��ʸ��ü��Σ�����˼�ǣ���5�˷�ȡ5Ǯ����������Ǯ�����γɵȲ����У�����ǰ2������Ǯ��֮�����3������Ǯ��֮����ȣ����������зֵ�Ǯ�������ǣ� ��
A.![]() Ǯ
Ǯ
B.1Ǯ
C.![]() Ǯ
Ǯ
D.![]() Ǯ
Ǯ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC1�� ![]() +
+ ![]() =1��ԲC2��x2+y2=t������ԲC1�Ľ��㣮
=1��ԲC2��x2+y2=t������ԲC1�Ľ��㣮
��1����PΪ��Բ������һ�㣬����P��ԲC2�����ߣ��е�ΪQ�����POQ�����ȡֵ��Χ������OΪ����ԭ�㣻
��2������M����1��0����ֱ��l������C1 �� C2���϶������ν��ڵ�A��B��C��D����|AB|=|CD|����ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У���������OΪ���ĵ����Σ�
�У���������OΪ���ĵ����Σ�![]() ����ABCD��
����ABCD��![]() ��
��![]() ��MΪBC��һ�㣮
��MΪBC��һ�㣮
![]() ��BM���ڶ���ʱ��
��BM���ڶ���ʱ��![]() ƽ��POM��
ƽ��POM��
![]() ������
������![]() �������£���
�������£���![]() ��������
��������![]() �������
�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ȥ�ꡰʮһ���ڼ䣬�������ٹ�·�����϶࣮ij���鹫˾�������շ�վ��7������С�������а����շ�վ���Ⱥ�˳��ÿ���50���ͳ�ȡһ���ij���������ȡ40���������г������飬��������ij�θ��ٹ�·�ij��٣�![]() ���ֳ����Σ�
���ֳ����Σ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��
�õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��
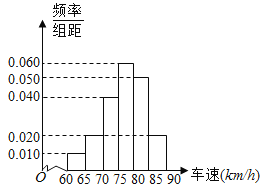
��I�����鹫˾�ڳ���ʱ�õ��������ֳ���������
��II������40��С���������ٵ���������λ���Ĺ���ֵ��
��III��������40��������![]() ��С�������������ȡ2����������2�������ٶ���
��С�������������ȡ2����������2�������ٶ���![]() �ĸ��ʣ�
�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�о�С�����о���ҹ�²��С�뻼��ð����֮��Ĺ�ϵ��ͳ�Ƶõ�1��6�·�ÿ��9�ŵ���ҹ�²�![]() ����ð�����������
����ð�����������![]() �����ݣ����±���
�����ݣ����±���
���� | 1��9�� | 2��9�� | 3��9�� | 4��9�� | 5��9�� | 6��9�� |
| 10 | 11 | 13 | 12 | 8 | 6 |
| 22 | 25 | 29 | 26 | 16 | 12 |
���о�С����о������ǣ��ȴ���6��������ѡȡ2�飬��ʣ�µ�4��������ع鷽�̣�����֮ǰ��ѡȡ��2�����ݽ��м���.
��1����ѡȡ1�º�6�µ�������Ϊ�������ݣ������ʣ�µ�2��5�µ����ݣ����![]() ����
����![]() �����Իع鷽�̣���������������������
�����Իع鷽�̣���������������������
��2�����ã�1��������Ļع鷽����Ԥ�����õ��Ĺ�����������ѡ���ļ������ݵ�������2�ˣ�����Ϊ�õ��Ļع鷽��������ģ����ʸ��о�С�����ûع鷽���Ƿ����룿
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com