
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() ,直线
,直线 ![]() .以极点
.以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的正半轴建立平面直角坐标系.
轴的正半轴建立平面直角坐标系.
(1)求直线![]() ,
,![]() 的直角坐标方程以及曲线
的直角坐标方程以及曲线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,直线
两点,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的面积.
的面积.
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知四棱台![]() 中,
中,![]() 平面ABCD,四边形ABCD为平行四边形,
平面ABCD,四边形ABCD为平行四边形,![]() ,
,![]() ,
,![]() ,
,![]() ,E为DC中点.
,E为DC中点.
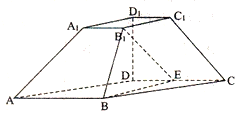
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)求三棱锥![]() 的高.
的高.
(注:棱台的两底面相似)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场有奖销售中,购满100元商品得1张奖券,多购多得,100张奖券为一个开奖单位,每个开奖单位设特等奖1个,一等奖10个,二等奖50个,设一张奖券中特等奖、一等奖、二等奖的事件分别为A,B,C,可知其概率平分别为![]()
![]()
![]() .
.
(1)求1张奖券中奖的概率;
(2)求1张奖券不中特等奖且不中一等奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见下表.
内,发布成绩使用等级制,各等级划分标准见下表.
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | A | B | C | D |
规定:A,B,C三级为合格等级,D为不合格等级为了解该校高三年级学生身体素质情况,从中抽取了n名学生的原始成绩作为样本进行统计.
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
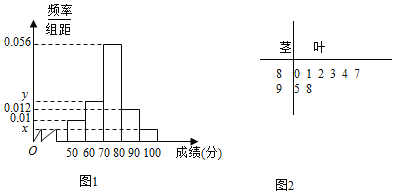
![]() 求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
![]() 根据频率分布直方图,求成绩的中位数
根据频率分布直方图,求成绩的中位数![]() 精确到
精确到![]() ;
;
![]() 在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的年收益![]() 与投资额
与投资额![]() 成正比,其关系如图1;投资股票等风险型产品的年收益
成正比,其关系如图1;投资股票等风险型产品的年收益![]() 与投资额
与投资额![]() 的算术平方根成正比,其关系如图2.
的算术平方根成正比,其关系如图2.

(1)分别写出两种产品的年收益![]() 和
和![]() 的函数关系式;
的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大年收益,其最大年收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用![]() 年的隔热层,每厘米厚的隔热层建造成本为
年的隔热层,每厘米厚的隔热层建造成本为![]() 万元.该建筑物每年的能源消耗费用
万元.该建筑物每年的能源消耗费用![]() (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度![]() (单位:厘米)满足关系:
(单位:厘米)满足关系:![]() .若不建隔热层,每年的能源消耗费用为
.若不建隔热层,每年的能源消耗费用为![]() 万元.设
万元.设![]() 为隔热层建造费用与
为隔热层建造费用与![]() 年的能源消耗费用之和.
年的能源消耗费用之和.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用![]() 最小,并求其最小值.
最小,并求其最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y2=4x的焦点为F,抛物线上有三个动点A,B,C.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,AB的垂直平分线经过一个定点Q,求△QAB面积的最大值.
,AB的垂直平分线经过一个定点Q,求△QAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场经销某商品,根据以往资料统计,顾客采用的付款期数![]() 的分布列为
的分布列为
| 1 | 2 | 3 | 4 | 5 |
| 0.2 | 0.3 | 0.3 | 0.1 | 0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为300元;分4期或5期付款,其利润为400元,![]() 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(1)求事件![]() :“购买该商品的3位顾客中,至少有1位采用期付款”的概率
:“购买该商品的3位顾客中,至少有1位采用期付款”的概率![]() ;
;
(2)求![]() 的分布列、期望和方差.
的分布列、期望和方差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com