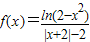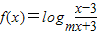
解:(I)f(x)是偶函数,证明如下:
当x>0 时,-x<0,有:f(x)=x
2+x-2
f(-x)=(-x)
2-(-x)-2=x
2+x-2=f(x);
当x<0 时,-x>0,有:f(x)=x
2-x-2
f(-x)=(-x)
2+(-x)-2=x
2-x-2=f(x);
当x=0,也有f(-x)=f(x),
又函数的定义域为R,关于原点对称,∴f(x)是偶函数;
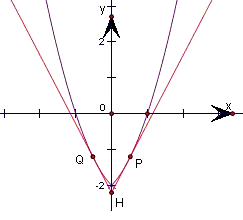
(II)画出函数f(x)的图象,如图所示,结合图象及(I)中结论可知,
若x
1≠x
2,且f(x
1)=f(x
2),则x
1和x
2关于原点O对称,
从而x
1+x
2=0,∴f(x
1+x
2)=-2;
(III)如图,根据对称性可知,当△PQH为正三角形时,切线PH的倾斜角为60°,
∴其斜率k=

,
当x>0时,f(x)=x
2+x-2,∴f′(x)=2x+1,
设P(m,n),则2m+1=

,且m
2+m-2=n,
解得:m=

,n=-

,
故切线PH的方程为:y+

=

(x-

),令x=0得y=

,
即h=

.
分析:(I)由已知易判断出函数的定义域为R,关于原点对称,再判断f(-x)与f(x)的关系,即可根据函数奇偶性的定义,进行判断得到结论;
(II)画出函数f(x)的图象,如图所示,结合图象及(I)中结论可知,若x
1≠x
2,且f(x
1)=f(x
2),则x
1和x
2关于原点O对称,从而求出f(x
1+x
2);
(III)如图,根据对称性可知,当△PQH为正三角形时,切线PH的倾斜角为60°,求出其斜率k,再结合导数几何意义求出点P(m,n)的坐标,从而得出切线PH的方程,最后令x=0即可.
点评:本小题主要考查分段函数的解析式求法及其图象的作法、函数奇偶性的判断、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

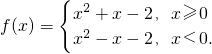
 解:(I)f(x)是偶函数,证明如下:
解:(I)f(x)是偶函数,证明如下: ,
, ,且m2+m-2=n,
,且m2+m-2=n, ,n=-
,n=- ,
, =
= (x-
(x- ),令x=0得y=
),令x=0得y= ,
, .
.