
已知以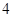 为周期的函数
为周期的函数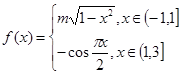 ,其中
,其中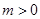 。若方程
。若方程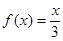 恰有5个实数解,则
恰有5个实数解,则 的取值范围为 ( )
的取值范围为 ( )
A.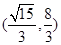 | B.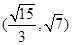 | C. | D.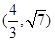 . . |
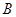
解析试题分析:∵当x∈(-1,1]时,将函数化为方程x2+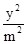 =1(y≥0),
=1(y≥0),
∴图象为半个椭圆,其图象如图所示,
同时在坐标系中作出当x∈(1,3]得图象,再根据周期性作出函数其它部分的图象,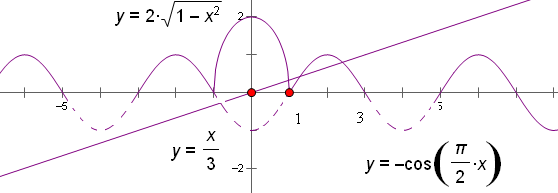
由图易知直线 y=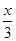 与第二个椭圆(x-4)2+
与第二个椭圆(x-4)2+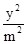 =1(y≥0)相交,而与第三个半椭圆(x-8)2+
=1(y≥0)相交,而与第三个半椭圆(x-8)2+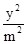 ="1" (y≥0)无公共点时,方程恰有5个实数解,
="1" (y≥0)无公共点时,方程恰有5个实数解,
将 y=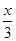 代入(x-4)2+
代入(x-4)2+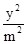 =1(y≥0)得,(9m2+1)x2-72m2x+135m2=0,令t=9m2(t>0),
=1(y≥0)得,(9m2+1)x2-72m2x+135m2=0,令t=9m2(t>0),
则(t+1)x2-8tx+15t=0,由△=(8t)2-4×15t (t+1)>0,得t>15,由9m2>15,且m>0得 m >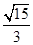 ,
,
同样将 y=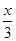 代入第三个椭圆方程(x-8)2+
代入第三个椭圆方程(x-8)2+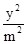 ="1" (y≥0),由△<0可计算得 m<
="1" (y≥0),由△<0可计算得 m<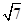 ,
,
综上可知m∈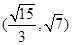 ,故选B。
,故选B。
考点:本题主要考查分段函数的概念及其图象,直线与椭圆的位置关系,函数的周期性。
点评:中档题,解的思路比较明确,首先数形结合,分析方程存在5个解时,的情况,通过建立方程组,利用判别式受到的限制进一步解题。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:单选题
如果函数
 =x
=x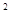 +2(a-1)x+2在区间(-∞,4)上是减函数,则实数a的取值范围是( )。
+2(a-1)x+2在区间(-∞,4)上是减函数,则实数a的取值范围是( )。
| A.a≥-3 | B. a≤-3 | C. a≤5 | D. a≥3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com