
已知两点M(-2,0),N(2,0),点P为坐标平面内的动点,且满足||||+·=0.
(1)求点P的轨迹C的方程;
(2)设过点N的直线l的斜率为k,且与曲线C相交于点S、T,若S、T两点只在第二象限内运动,线段ST的垂直平分线交x轴于Q点,求Q点横坐标的取值范围.
(1) y2=-8x
(2) (-∞,-6)
【解析】(1)设点P(x,y),根据题意则有:
=(4,0),||=4,||=,=(x-2,y),
代入||||+·=0,得:4+4(x-2)=0.
整理得点P的轨迹C的方程:y2=-8x.
(2)设S(x1,y1),T(x2,y2),
由题意得:ST的方程为y=k(x-2)(显然k≠0)
与y2=-8x联立消元得:ky2+8y+16k=0,
则有:y1+y2=-,y1y2=16.
因为直线交轨迹C于两点,
则Δ=b2-4ac=64-64k2>0,
再由y1>0,y2>0,则->0,故-1<k<0.
可求得线段ST中点B的坐标为(-+2,-),
所以线段ST的垂直平分线方程为
y+=-(x+-2).令y=0得点Q横坐标为xQ=-2-,
xQ=-2-<-6.,所以Q点横坐标的取值范围为(-∞,-6).


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
| PM |
| PN |
A、
| ||
| B、x2+y2=16 | ||
| C、y2-x2=8 | ||
| D、x2+y2=8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| MN |
| MP |
| MN |
| NP |
| A、y2=8x |
| B、y2=-8x |
| C、y2=4x |
| D、y2=-4x |
查看答案和解析>>
科目:高中数学 来源: 题型:
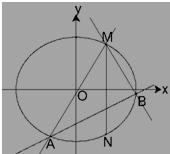 已知两点M(2,3),N(2,-3)在椭圆C:
已知两点M(2,3),N(2,-3)在椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| MN |
| MP |
| MN |
| MP |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com