
【题目】已知函数f(x)= ![]() +bx(其中a,b为常数)的图象经过(1,3)、(2,3)两点.
+bx(其中a,b为常数)的图象经过(1,3)、(2,3)两点.
(I)求a,b的值,判断并证明函数f(x)的奇偶性;
(II)证明:函数f(x)在区间[ ![]() ,+∞)上单调递增.
,+∞)上单调递增.
【答案】解:(Ⅰ)∵函数f(x)的图象经过(1,3)、(2,3)两点
∴ 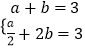 ,得a=2,b=1,
,得a=2,b=1,
∴函数解析 ![]() ,定义域为:(﹣∞,0)∪(0,+∞),关于原点对称,
,定义域为:(﹣∞,0)∪(0,+∞),关于原点对称,
又∵ ![]() ,
,
∴函数f(x)是奇函数;
(II)设任意的 ![]() ,且x1<x2,
,且x1<x2,
∵ ![]()
= ![]()
∵ ![]() ,
,
∴x2﹣x1>0,且2﹣x1x2<0,
所以f(x1)﹣f(x2)<0,即f(x1)<f(x2),
∴函数f(x)在区间 ![]() 上单调递增.
上单调递增.
【解析】本题考查的是用定义去证明函数的单调性,根据奇偶性去解决问题。
【考点精析】认真审题,首先需要了解函数单调性的判断方法(单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较),还要掌握函数的奇偶性(偶函数的图象关于y轴对称;奇函数的图象关于原点对称)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2bx,g(x)=|x﹣1|,若对任意x1 , x2∈[0,2],当x1<x2时都有f(x1)﹣f(x2)<g(x1)﹣g(x2),则实数b的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且对任意的n∈N*都有Sn=2an﹣n,
(1)求数列{an}的前三项a1 , a2 , a3;
(2)猜想数列{an}的通项公式an , 并用数学归纳法证明;
(3)求证:对任意n∈N*都有 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆C过点M(5,2),N(3,2)且圆心在x轴上,点A为圆C上的点,O为坐标原点.
(1)求圆C的方程;
(2)连接OA,延长OA到P,使得|OA|=|AP|,求点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本C(x),当年产量不足80千件时,C(x)= ![]() x2+10x(万元);当年产量不小于80千件时C(x)=51x+
x2+10x(万元);当年产量不小于80千件时C(x)=51x+ ![]() ﹣1450(万元),通过市场分析,若每件售价为500元时,该厂本年内生产该商品能全部销售完.
﹣1450(万元),通过市场分析,若每件售价为500元时,该厂本年内生产该商品能全部销售完.
(1)写出年利润L(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为y=2x2+1,值域为{5,19}的“孪生函数”共有( )
A.4个
B.6个
C.8个
D.9个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在多面体ABCDE中,BC=BA,DE∥BC,AE⊥平面BCDE,BC=2DE,F为AB的中点. 
(1)求证:EF∥平面ACD;
(2)若EA=EB=CD,求二面角B﹣AD﹣E的正切值的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com