过双曲线x2-y2=1上一点Q作直线x+y=2的垂线,垂足为N,则线段QN的中点P的轨迹方程为( )
A.2x2-2y2-2x-1=0
B.x2+y2=1
C.2x2+2y2-y=0
D.2x2-2y2-2x+2y-1=0
【答案】
分析:设P(x,y),欲求其轨迹方程,即寻找其坐标间的关系,根据垂线的关系及点Q在双曲线上,代入其方程即可得到.
解答:解:设P(x,y),Q(x
1,y
1),则N(2x-x
1,2y-y
1),
∵N在直线x+y=2上,
∴2x-x
1+2y-y
1=2①
又∵PQ垂直于直线x+y=2,∴
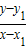
=1,
即x-y+y
1-x
1=0.②
由①②得
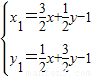
,
又∵Q在双曲线x
2-y
2=1上,
∴x
12-y
12=1.
∴(

x+

y-1)
2-(

x+

y-1)
2=1.
整理,得2x
2-2y
2-2x+2y-1=0即为中点P的轨迹方程.
故选D.
点评:本题主要考查了轨迹方程的问题.求曲线的轨迹方程是解析几何的基本问题.代入法:动点所满足的条件不易表述或求出,但形成轨迹的动点P(x,y)却随另一动点Q(x′,y′)的运动而有规律的运动,且动点Q的轨迹为给定或容易求得,则可先将x′,y′表示为x,y的式子,再代入Q的轨迹方程,然而整理得P的轨迹方程,代入法也称相关点法.

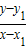 =1,
=1,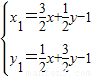 ,
, x+
x+ y-1)2-(
y-1)2-( x+
x+ y-1)2=1.
y-1)2=1.

 阅读快车系列答案
阅读快车系列答案