
| |||||||||||||||
(1) |
解析:椭圆C的焦点在x轴上,由椭圆上的点A到F1、F2两点的距离之和是4,得2a=4,即a=2. 又点A(1, 所以椭圆C的方程为 |
(2) |
设椭圆C上的动点为K(x1,y1),线段F1K的中点Q(x,y)满足x= 因此 |
(3) |
类似的性质为:若M、N是双曲线 设点M的坐标为(m,n),则点N的坐标为(-m,-n),其中 又设点P的坐标为(x,y),由kPM= 点评:本题主要考查椭圆的基本知识及求动点轨迹方程的常用方法.第(3)问对考生的联想、类比、逻辑思维及运算能力都有较高的要求,根据提供的信息,让考生通过类比自己找到所证问题,这是高考数学命题的方向.应引起注意. |


科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (a>b>0)的左、右两个焦点,椭圆C上的点
(a>b>0)的左、右两个焦点,椭圆C上的点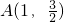 到两点的距离之和等于4.
到两点的距离之和等于4. 求|PQ|的最大值.
求|PQ|的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com