直线ax+by+c=0(ab≠0)截圆x2+y2=5所得弦长等于4,则以|a|、|b|、|c|为边长的确定三角形一定是 .
【答案】
分析:由弦长的一半,圆的半径,利用勾股定理求出弦心距d,即为圆心到已知直线的距离,利用点到直线的距离公式列出关系式,整理后得到a
2+b
2=c
2,根据勾股定理的逆定理可得出此三角形为直角三角形.
解答:解:∵直线ax+by+c=0(ab≠0)截圆x
2+y
2=5所得弦长等于4,圆的半径r=
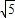
,
∴弦心距d=
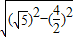
=1,
即圆心到直线ax+by+c=0的距离
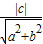
=1,
整理得:a
2+b
2=c
2,
则以|a|、|b|、|c|为边长的确定三角形一定是直角三角形.
故答案为:直角三角形
点评:此题考查了三角形形状的判断,以及直线与圆相交的性质,涉及的知识有:垂径定理,勾股定理及逆定理,以及点到直线的距离公式,当直线与圆相交时,常常利用垂径定理由垂直得中点,利用弦长的一半,圆的半径及弦心距构造直角三角形,利用勾股定理来解决问题.

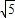 ,
,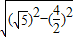 =1,
=1,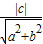 =1,
=1,

 阅读快车系列答案
阅读快车系列答案