
分析 (1)求导,分类讨论,根据导数与函数单调性求得关系,即可求得f(x)的单调性;
(2)求导,原不等式x2≤2x+ax2+$\frac{{x}^{2}+ax+{a}^{2}+1}{a}$,对任意a>0恒成立,整理得:a+$\frac{1}{a}$≥$\frac{{x}^{2}-3x}{{x}^{2}+1}$(a>0),利用基本不等式性质,即可求得$\frac{{x}^{2}-3x}{{x}^{2}+1}$≤2,即可求得实数x的取值范围.
解答 解:(1)求导,f'(x)=2xeax+ax2eax=(2x+ax2)eax.
当a=0时,若x<0,则f'(x)<0,若x>0,则f'(x)>0.
∴当a=0时,函数f(x)在区间(-∞,0)内为减函数,在区间(0,+∞)内为增函数.
当a>0时,由2x+ax2>0,解得x<-$\frac{2}{a}$或x>0,
由2x+ax2<0,解得-$\frac{2}{a}$<x<0.
∴当a>0时,函数f(x)在区间(-∞,-$\frac{2}{a}$)内为增函数,在区间(-$\frac{2}{a}$,0)内为减函数,在区间(0,+∞)内为增函数;
当a<0时,由2x+ax2>0,解得0<x<-$\frac{2}{a}$,
由2x+ax2<0,解得x<0或x>-$\frac{2}{a}$.
∴当a<0时,函数f(x)在区间(-∞,0)内为减函数,在区间(0,-$\frac{2}{a}$)内为增函数,在区间(-$\frac{2}{a}$,+∞)内为减函数;
综上可知:当a=0时,函数f(x)在区间(-∞,0)内为减函数,在区间(0,+∞)内为增函数;
当a>0时,函数f(x)在区间(-∞,-$\frac{2}{a}$)内为增函数,在区间(-$\frac{2}{a}$,0)内为减函数,在区间(0,+∞)内为增函数;
当a<0时,函数f(x)在区间(-∞,0)内为减函数,在区间(0,-$\frac{2}{a}$)内为增函数,在区间(-$\frac{2}{a}$,+∞)内为减函数;
(2)由题意可知:对任意a>0,x2eax≤2xeax+ax2eax+$\frac{{x}^{2}+ax+{a}^{2}+1}{a}$eax恒成立,
即x2≤2x+ax2+$\frac{{x}^{2}+ax+{a}^{2}+1}{a}$,对任意a>0恒成立,
则(a+$\frac{1}{a}$)(x2+1)≥x2-3x,即a+$\frac{1}{a}$≥$\frac{{x}^{2}-3x}{{x}^{2}+1}$(a>0),
由a+$\frac{1}{a}$≥2$\sqrt{a•\frac{1}{a}}$=2,当且仅当a=$\frac{1}{a}$时,即a=1时,取最小值,
则$\frac{{x}^{2}-3x}{{x}^{2}+1}$≤2,解得:x≤-2或x≥-1,
综上可知:x的取值范围为(-∞,-2]∪[-1,+∞).
点评 本题考查导数的综合应用,考查导数与函数的关系,基本不等式的性质,考查分类讨论思想及转化思想,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
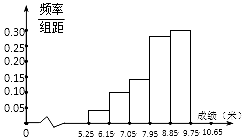 某校举行运动会,其中三级跳远的成绩在8.0米 (四舍五入,精确到0.1米) 以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某校举行运动会,其中三级跳远的成绩在8.0米 (四舍五入,精确到0.1米) 以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.6 | B. | 0.48 | C. | 0.75 | D. | 0.56 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-y=0 | B. | 2x-y-2=0 | C. | x+2y-3=0 | D. | x-2y+3=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{17}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com