
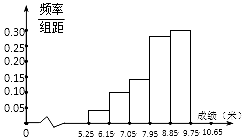
 某校举行运动会,其中三级跳远的成绩在8.0米 (四舍五入,精确到0.1米) 以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某校举行运动会,其中三级跳远的成绩在8.0米 (四舍五入,精确到0.1米) 以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.分析 (1)由频率分直方图求出第6小组的频率,从而求出总人数,进而得到第4、5、6组成绩均进入决赛,由此能求出进入决赛的人数.
(2)设甲、乙各跳一次的成绩分别为x、y米,则基本事件满足的区域为:$\left\{\begin{array}{l}{8≤x≤10}\\{9.5≤y≤10.5}\end{array}\right.$,由此利用几何概型能求出甲比乙远的概率.
解答 解:(1)第6小组的频率为1-(0.04+0.10+0.14+0.28+0.30)=0.14,
∴总人数为$\frac{7}{0.14}$=50(人).…(2分)
∴第4、5、6组成绩均进入决赛,人数为(0.28+0.30+0.14)×50=36(人)
即进入决赛的人数为36.…(6分)
(2)设甲、乙各跳一次的成绩分别为x、y米,则基本事件满足的区域为$\left\{\begin{array}{l}{8≤x≤10}\\{9.5≤y≤10.5}\end{array}\right.$,
事件A“甲比乙远的概率”满足的区域为x>y,如图所示.…(10分)
∴由几何概型P(A)=$\frac{\frac{1}{2}×\frac{1}{2}×\frac{1}{2}}{1×2}$=$\frac{1}{16}$.即甲比乙远的概率为$\frac{1}{16}$.…(12分)
点评 本题考查频率分布直方图的应用,考查概率的求法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 集合M={x|0<x≤3},N={x|0<x≤2},则“a∈M”是“a∈N”的充分不必要条件 | |
| B. | 命题“若a∈M,则b∉M”的否命题是“若a∉M,则b∈M” | |
| C. | “|a|>|b|”是“a2>b2”的必要不充分条件 | |
| D. | 命题“若a,b都是奇数,则a+b是偶数”的逆否命题是“若a+b不是偶数,则a,b都不是奇数” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com