
分析 (Ⅰ)利用公式直接计算可知数列{an}的通项公式,通过作差可知$\frac{{b}_{n+1}}{n+1}=\frac{{b}_{n}}{n}$,进而可得bn=n;
(Ⅱ)通过(1)可知anbn=n•2n,即可利用错位相加法计算数列的和.
解答 解:(Ⅰ)由a1=2,an+1=2an,得:${a}_{n}={2}^{n}$;
由b1=1,b1+$\frac{1}{2}$b2+$\frac{1}{3}$b3+…+$\frac{1}{{b}_{n}}$=bn+1-1知,
当n=1时,b1=b2-1,故b2=2.
当n≥2时,$\frac{1}{n}{b}_{n}={b}_{n+1}-{b}_{n}$,整理得:$\frac{{b}_{n+1}}{{b}_{n}}=\frac{n+1}{n}$,
∴$\frac{{b}_{2}}{{b}_{1}}=\frac{2}{1}$,$\frac{{b}_{3}}{{b}_{2}}=\frac{3}{2}$,…,$\frac{{b}_{n}}{{b}_{n-1}}=\frac{n}{n-1}$(n≥2).
累积可得:bn=n,
验证b1=1成立,
∴bn=n;
(Ⅱ)由(1)知,${a}_{n}{b}_{n}=n•{2}^{n}$,
∴数列{anbn}的前n项和为Tn=2+2×22+3×23+…+n×2n,
$2{T}_{n}={2}^{2}+2×{2}^{3}+3×{2}^{4}+…+(n-1)×{2}^{n}+n×{2}^{n+1}$,
作差可得:$-{T}_{n}=2+{2}^{2}+{2}^{3}+…+{2}^{n}-n×{2}^{n+1}$=$\frac{2(1-{2}^{n})}{1-2}-n×{2}^{n+1}$=2n+1-2-n×2n+1,
∴${T}_{n}=(n-1)×{2}^{n+1}+2$.
点评 本题考查数列的递推关系式,训练了错位相减法求数列的和,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
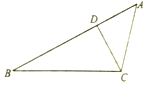 如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.
如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
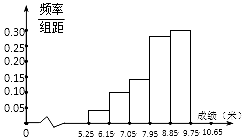 某校举行运动会,其中三级跳远的成绩在8.0米 (四舍五入,精确到0.1米) 以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某校举行运动会,其中三级跳远的成绩在8.0米 (四舍五入,精确到0.1米) 以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)<ef(0),f(2017)>e2017f(0) | B. | f(1)>ef(0),f(2017)>e2017f(0) | ||
| C. | f(1)>ef(0),f(2017)<e2017f(0) | D. | f(1)<ef(0),f(2017)<e2017f(0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.6 | B. | 0.48 | C. | 0.75 | D. | 0.56 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{17}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com