
分析 (1)利用等差数列的通项公式列出方程组,求出首项和公差,由此能求出数列{an}的通项公式.
(2)由${S}_{n}=-{n}^{2}+5n$=-(n-$\frac{5}{2}$)2+$\frac{25}{4}$,能求出Sn的最大值.
解答 解:(1)设等差数列{an}中首项为a1,公差为d.
因为a7=-8,a17=-28,
所以$\left\{\begin{array}{l}{{a}_{1}+6d=-8}\\{{a}_{1}+16d=-28}\end{array}\right.$,
解得a1=4,d=-2,
所以an=a1+(n-1)d=-2n+6.
(2)由(1)可得${S}_{n}=-{n}^{2}+5n$=-(n-$\frac{5}{2}$)2+$\frac{25}{4}$,
所以当n=2或n=3时,Sn取得最大值.
(Sn)max=-22+2×5=-32+3×5=6.
点评 本题考查等差数列的通项公式的求法,考查等差数列的前n项和的最大值的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 将图象上的每一点横坐标缩短到原来的$\frac{1}{2}$而纵坐标不变 | |
| B. | 沿x向左平移$\frac{π}{2}$个单位,再把得图象上的每一点横坐标伸长到原来的2而纵坐标不变 | |
| C. | 先把图象上的每一点横坐标缩短到原来的$\frac{1}{2}$而纵坐标不变,再将所得图象沿x向右平移$\frac{π}{4}$个单位 | |
| D. | 先把图象上的每一点横坐标缩短到原来的$\frac{1}{2}$而纵坐标不变,再将所得图象沿x向左平移$\frac{π}{2}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
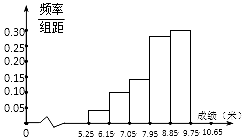 某校举行运动会,其中三级跳远的成绩在8.0米 (四舍五入,精确到0.1米) 以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某校举行运动会,其中三级跳远的成绩在8.0米 (四舍五入,精确到0.1米) 以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)<ef(0),f(2017)>e2017f(0) | B. | f(1)>ef(0),f(2017)>e2017f(0) | ||
| C. | f(1)>ef(0),f(2017)<e2017f(0) | D. | f(1)<ef(0),f(2017)<e2017f(0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.6 | B. | 0.48 | C. | 0.75 | D. | 0.56 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com