
分析 (Ⅰ)按照x与1进行讨论,分离常数得a≤$\frac{{x}^{2}-1}{|x-1|}$,令φ(x)=$\frac{{x}^{2}-1}{|x-1|}$,去掉绝对值符号化简解析式,由一次函数的性质分别求出φ(x)的范围,由恒成立问题求出a的范围,最后取并集;
(Ⅱ)由题意求出h(x),求出对称轴,由区间和对称轴对a进行分类讨论,分别由二次函数的性质判断出h(x)在区间上的单调性,并求出对应的最大值.
解答 (本题满分为15分)
解:(Ⅰ)不等式f(x)≥g(x)对x∈R恒成立,即(x2-1)≥a|x-1|(*)对x∈R恒成立,
①当x=1时,(*)显然成立,此时a∈R; …(2分)
②当x≠1时,(*)可变形为a≤$\frac{{x}^{2}-1}{|x-1|}$,令φ(x)=$\frac{{x}^{2}-1}{|x-1|}$=$\left\{\begin{array}{l}{x+1}&{x>1}\\{-(x+1)}&{x<1}\end{array}\right.$,
因为当x>1时,φ(x)>2,当x<1时,φ(x)>-2,…(4分)
所以φ(x)>-2,故此时a≤-2.
综合①②,得所求实数a的取值范围是a≤-2.…(6分)
(Ⅱ)$h(x)=\left\{\begin{array}{l}-{x^2}-ax+a+1,0≤x<1\\ 0,{\;}^{\;}{\;}^{\;}{\;}^{\;}{\;}^{\;}{\;}^{\;}x=1\\{x^2}+ax-a-1,1<x≤2\end{array}\right.$,…(7分)
∵a≤0,
∴$对称轴x=-\frac{a}{2}≥0$,
①当$0≤-\frac{a}{2}≤1$时,即-2≤a≤0,${(-{x^2}-ax+a+1)_{max}}=h(-\frac{a}{2})=\frac{a^2}{4}+a+1$(x2+ax-a-1)max=h(2)=a+3,
∵$\frac{a^2}{4}+a+1-(a+3)=\frac{{{a^2}-8}}{4}<0$,
∴h(x)max=a+3,…(9分)
②当$1<-\frac{a}{2}≤2$时,即-4≤a<-2,(-x2-ax+a+1)max=h(1)=0,${({x^2}+ax-a-1)_{max}}=max\{h(1),h(2)\}=max\{0,3+a\}=\left\{\begin{array}{l}0,-4≤a<-3\\ 3+a,-3≤a<-2\end{array}\right.$,
此时$h{(x)_{max}}=\left\{\begin{array}{l}0,-4≤a<-3\\ 3+a,-3≤a<-2\end{array}\right.$,…(11分)
③当$-\frac{a}{2}>2$时,即a<-4,(-x2-ax+a+1)max=h(1)=0(x2+ax-a-1)max=h(1)=0,
此时h(x)max=0,…(13分)
综上:h(x)max=t(a)=$\left\{\begin{array}{l}3+a,-3≤a≤0\\ 0,a<-3\end{array}\right.$,
∴t(a)min=0.…(15分)
点评 本题考查函数的零点与方程的根的关系,解题的关键是根据所给的条件及相关知识对问题进行正确转化,本题比较抽象,对问题的转化尤其显得重要,本题在求解问题时用到了分类讨论的思想,转化化归的思想,数学综合题的求解过程中,常用到这两个思想,繁杂的分类使得该题难度较大.


科目:高中数学 来源: 题型:选择题
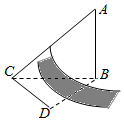 如图,测量河对岸的旗杆AB高时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=a,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )
如图,测量河对岸的旗杆AB高时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=a,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )| A. | $\frac{{\sqrt{2}}}{2}a$ | B. | $\frac{{3\sqrt{2}}}{2}a$ | C. | $\frac{{\sqrt{3}}}{2}a$ | D. | $\frac{{\sqrt{6}}}{2}a$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.
如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
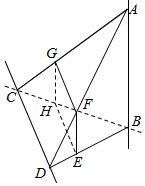 如图所示,异面直线AB,CD互相垂直,AB=$\sqrt{6}$,BC=$\sqrt{3}$,CD=1,BD=2,AC=3,截面EFGH分别与BD,AD,AC,BC相交于点E,F,G,H,且AB∥平面EFGH,CD∥平面EFGH.
如图所示,异面直线AB,CD互相垂直,AB=$\sqrt{6}$,BC=$\sqrt{3}$,CD=1,BD=2,AC=3,截面EFGH分别与BD,AD,AC,BC相交于点E,F,G,H,且AB∥平面EFGH,CD∥平面EFGH.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{b}{a}$<$\frac{b+m}{a+m}$ | B. | $\frac{b}{a}$>$\frac{b+m}{a+m}$ | C. | $\frac{b}{a}$=$\frac{b+m}{a+m}$ | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
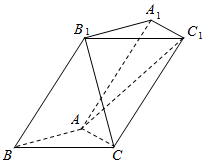 如图,在三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,BB1=2,∠ABB1=60°.
如图,在三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,BB1=2,∠ABB1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (0,1)∪(2,+∞) | C. | (-∞,0)∪(0,2) | D. | (-∞,0)∪(2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com