
 (2012•威海二模)如图,菱形ABCD的边长为2,∠A=60°,M为DC的中点,若N为菱形内任意一点(含边界),则
(2012•威海二模)如图,菱形ABCD的边长为2,∠A=60°,M为DC的中点,若N为菱形内任意一点(含边界),则| AM |
| AN |
| AM |
| AN |
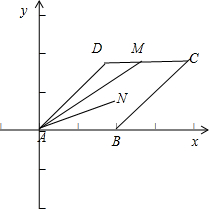 解::以点A位坐标原点建立如图所示的直角坐标系,由于菱形ABCD的边长为2,∠A=60°,M为DC的中点,
解::以点A位坐标原点建立如图所示的直角坐标系,由于菱形ABCD的边长为2,∠A=60°,M为DC的中点,| 3 |
| 3 |
| 3 |
| AM |
| 3 |
| AN |
| AM |
| AN |
| 3 |
| 3 |
| 3 |
| 3 |


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 512 |
| a | 2 n |
| a | 2 n+1 |
| T | n |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•威海二模)如图,边长为2的正方形内有一不规则阴影部分,随机向正方形内投入200粒芝麻,恰有60粒落入阴影部分,则不规则图形的面积为( )
(2012•威海二模)如图,边长为2的正方形内有一不规则阴影部分,随机向正方形内投入200粒芝麻,恰有60粒落入阴影部分,则不规则图形的面积为( )查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 4 |
| x+ξ |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•威海二模)某商场调查旅游鞋的销售情况,随机抽取了部分顾客的购鞋尺寸,整理得如下频率分布直方图,其中直方图从左至右的前3个小矩形的面积之比为1:2:3,则购鞋尺寸在[39.5,43.5)内的顾客所占百分比为
(2012•威海二模)某商场调查旅游鞋的销售情况,随机抽取了部分顾客的购鞋尺寸,整理得如下频率分布直方图,其中直方图从左至右的前3个小矩形的面积之比为1:2:3,则购鞋尺寸在[39.5,43.5)内的顾客所占百分比为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com