
分析 (1)定义域容易求出为[-$\frac{1}{2}$,+∞);
(2)可看出x增大时,f(x)增大,从而判断出f(x)在$[-\frac{1}{2},+∞)$上单调递增,根据增函数的定义,设任意的${x}_{1}>{x}_{2}≥-\frac{1}{2}$,然后作差,分子有理化,提取公因式x1-x2,从而证明f(x1)>f(x2)便可得出f(x)的单调性.
解答 解:(1)要使f(x)有意义,则1+2x≥0;
∴$x≥-\frac{1}{2}$;
∴f(x)的定义域为[$-\frac{1}{2}$,+∞);
(2)x增大时,f(x)增大,∴f(x)在$[-\frac{1}{2},+∞)$上单调递增,证明如下:
$设{x}_{1}>{x}_{2}≥-\frac{1}{2}$,则:
$f({x}_{1})-f({x}_{2})={x}_{1}+\sqrt{1+2{x}_{1}}-{x}_{2}-\sqrt{1+2{x}_{2}}$=$({x}_{1}-{x}_{2})+\frac{2({x}_{1}-{x}_{2})}{\sqrt{1+2{x}_{1}}+\sqrt{1+2{x}_{2}}}$=$({x}_{1}-{x}_{2})(1+\frac{2}{\sqrt{1+2{x}_{1}}+\sqrt{1+2{x}_{2}}})$;
∵${x}_{1}>{x}_{2}≥-\frac{1}{2}$;
∴x1-x2>0,$1+\frac{2}{\sqrt{1+2{x}_{1}}+\sqrt{1+2{x}_{2}}}>0$;
∴f(x1)>f(x2);
∴f(x)在$[-\frac{1}{2},+∞)$上单调递增.
点评 考查函数定义域的概念及求法,函数单调性的定义,根据单调性定义判断并证明一个函数的单调性的方法和过程,作差的方法比较f(x1),f(x2),分子有理化的运用,作差后一般要提取公因式x1-x2.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
 如图,底角∠ABE=45°的直角梯形ABCD,底边BC长为4cm,腰长AB为$2\sqrt{2}$cm,当一条垂直于底边BC的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BE=x,试写出阴影部分的面积y与x的函数关系式,并画出函数大致图象.
如图,底角∠ABE=45°的直角梯形ABCD,底边BC长为4cm,腰长AB为$2\sqrt{2}$cm,当一条垂直于底边BC的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BE=x,试写出阴影部分的面积y与x的函数关系式,并画出函数大致图象.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{2}{3},+∞)$ | B. | (1,+∞) | C. | $[{\frac{2}{3},1}]$ | D. | $(\frac{2}{3},\left.1]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\sqrt{3}$ | C. | -2$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
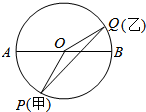 如图,有一个半径为20m的圆形水池,甲、乙两人分别从水池一条直径AB的两端开始,同时按逆时针方向绕水池边缘做匀速圆周运动,已知乙绕水池2圈需要1min,甲的速度是乙的两倍.如果从两人出发时开始计时,求当乙绕水池1周的过程中,两人的直线距离l(m)和时间t(s)的函数关系式.
如图,有一个半径为20m的圆形水池,甲、乙两人分别从水池一条直径AB的两端开始,同时按逆时针方向绕水池边缘做匀速圆周运动,已知乙绕水池2圈需要1min,甲的速度是乙的两倍.如果从两人出发时开始计时,求当乙绕水池1周的过程中,两人的直线距离l(m)和时间t(s)的函数关系式.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com