
【题目】将![]() 方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )
方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )
A.33B.56C.64D.78
【答案】B
【解析】
记分隔边的条数为![]() ,首先将方格表按图分成三个区域,, 分别染成三种颜色, 粗线上均为分隔边,将方格表的行从上至下依次记为
,首先将方格表按图分成三个区域,, 分别染成三种颜色, 粗线上均为分隔边,将方格表的行从上至下依次记为![]() ,列从左至右依次记为
,列从左至右依次记为![]() ,行
,行![]() 中方格出现的颜色为
中方格出现的颜色为![]() ,列
,列![]() 中方格出现的颜色为
中方格出现的颜色为![]() ,三种颜色分别记为
,三种颜色分别记为![]() ,对于一种颜色
,对于一种颜色![]() ,设
,设![]() 为含色方格的行数与列数之和,定义当
为含色方格的行数与列数之和,定义当![]() 行含
行含![]() 色方格时,
色方格时,![]() ,否则
,否则![]() ,类似的定义
,类似的定义![]() ,计算得到
,计算得到![]() ,再证明
,再证明![]() ,再证明对任意
,再证明对任意![]() 均有
均有![]() ,
,![]() ,最后求出分隔边条数的最小值.
,最后求出分隔边条数的最小值.
记分隔边的条数为![]() ,首先将方格表按图分成三个区域,如图:
,首先将方格表按图分成三个区域,如图:
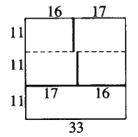
分别染成三种颜色,粗线上均为分隔边,此时共有56条分隔边,则![]() ,
,
其次证明:![]() ,
,
将方格表的行从上至下依次记为![]() ,列从左至右依次记为
,列从左至右依次记为![]() ,
,
行![]() 中方格出现的颜色为
中方格出现的颜色为![]() ,列
,列![]() 中方格出现的颜色为
中方格出现的颜色为![]() ,
,
三种颜色分别记为![]() ,对于一种颜色
,对于一种颜色![]() ,设
,设![]() 为含色方格的行数与列数之和,
为含色方格的行数与列数之和,
定义当![]() 行含
行含![]() 色方格时,
色方格时,![]() ,否则
,否则![]() ,
,
类似的定义![]() ,
,
所以![]()
![]() ,
,
由于染![]() 色的格的行有
色的格的行有![]() 个,列有
个,列有![]() 个,则
个,则![]() 色的方格一定在这
色的方格一定在这![]() 行和
行和![]() 列的交叉方格中,从而
列的交叉方格中,从而![]() ,
,
所以![]()
![]() 所以①,
所以①,
由于在行![]() 中有
中有![]() 种颜色的方格,于是至少有
种颜色的方格,于是至少有![]() 条分隔边,
条分隔边,
类似地,在列![]() 中至少有
中至少有![]() 条分隔边,
条分隔边,
则![]()
![]() ②
②
![]() ③,
③,
下面分两种情况讨论:
1、有一行或一列所有方格同色,不妨设为![]() 色,则方格表的33列中均含有
色,则方格表的33列中均含有![]() 色的方格,又
色的方格,又![]() 色的方格有363个,
色的方格有363个,
故至少有![]() 行含有
行含有![]() 色的方格,于是
色的方格,于是![]() ④,
④,
由①③④得![]() ;
;
2、没有一行也没有一列所有方格同色,对任意![]() 均有
均有![]() ,
,![]() ,
,
从而由②可得![]() ;
;
综上所述,分隔边条数的最小值为56.
故选:B


科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2,对任意的x∈[t,t+2]不等式f(x+t)≥2f(x)恒成立,那么实数t的取值范围是( )
A. [![]() ,+∞) B. [2,+∞) C. (0,
,+∞) B. [2,+∞) C. (0,![]() ] D. [0,
] D. [0,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只红蚂蚁与一只黑蚂蚁在一个单位圆(半径为1的圆)上爬动,若两只蚂蚁均从点A(1,0)同时逆时针匀速爬动,若红蚂蚁每秒爬过α角,黑蚂蚁每秒爬过β角(其中0°<α<β<180°),如果两只蚂蚁都在第14秒时回到A点,并且在第2秒时均位于第二象限,求α,β的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设n为给定的大于2的整数。有n个外表上没有区别的袋子,第k(k=1,2,···,n)个袋中有k个红球,n-k个白球。将这些袋子混合后,任选一个袋子,并且从中连续取出三个球(每次取出不放回)。求第三次取出的为白球的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值.求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,点B是
的直径,点B是![]() 上与A,C不重合的动点,
上与A,C不重合的动点,![]() 平面
平面![]() .
.

(1)当点B在什么位置时,平面![]() 平面
平面![]() ,并证明之;
,并证明之;
(2)请判断,当点B在![]() 上运动时,会不会使得
上运动时,会不会使得![]() ,若存在这样的点B,请确定点B的位置,若不存在,请说明理由.
,若存在这样的点B,请确定点B的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体![]() 的长,宽,高分别为4,3,5,现有一甲壳虫从
的长,宽,高分别为4,3,5,现有一甲壳虫从![]() 点出发沿长方体表面爬行到
点出发沿长方体表面爬行到![]() 点来获取食物.
点来获取食物.
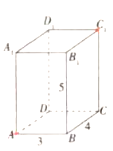
(1)甲壳虫想尽快获取食物可通过哪些路径获取?
(2)哪条获取食物的路径最短?最短为多少?
(3)此类问题的一般处理方法是什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com