
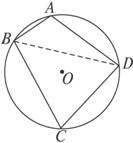
解:如图,连结BD,则有四边形ABCD的面积S=S△ABD+S△CDB=![]() AB·ADsinA+
AB·ADsinA+![]() BC·CDsinC.
BC·CDsinC.
∵A+C=180°,∴sinA=sinC.
故S=![]() (AB·AD+BC·CD)·sinA=
(AB·AD+BC·CD)·sinA=![]() (2×4+6×4)sinA=16sinA.
(2×4+6×4)sinA=16sinA.
由余弦定理,在△ABD中,BD2=AB2+AD2-2AB·ADcosA=20-16cosA;
在△CDB中,BD2=CB2+CD2-2CB·CDcosC=52-48cosC.
∴20-16cosA=52-48cosC.
∵cosC=-cosA,
∴64cosA=-32,cosA=-![]() .
.
又0°<A<180°,
∴A=120°.故S=16sin120°=8![]() .
.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源:江苏省私立无锡光华学校2009—2010学年高二第二学期期末考试 题型:解答题
本题满分16分)已知圆内接四边形ABCD的边长分别为AB = 2,BC = 6,CD = DA = 4;求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com