
某市为了解社区群众体育活动的开展情况,拟采用分层抽样的方法从A,B,C三个行政区抽出6个社区进行调查.已知A,B,C行政区中分别有12,18,6个社区.
(1)求从A,B,C三个行政区中分别抽取的社区个数;
(2)若从抽得的6个社区中随机的抽取2个进行调查结果的对比,求抽取的2个社区中至少有一个来自A行政区的概率.
(1)2,3,1(2)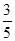
解析试题分析:
(1)根据分层抽样的原理,在抽样的过程中保持每个个体被抽到的概率相等,按照人数的比列把抽样的人数分到相应的层,则有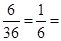
 ,即可求出每层应该抽取的人数.
,即可求出每层应该抽取的人数.
(2)首先对抽取的6个社区进行编号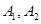 ,
,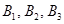 ,
,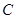 ,则列出从6个社区中选取两个的所有基本事件数为15,在所有的基本事件中找出满足至少有一个来自A社区的基本事件数为9,再根据古典概型的概率计算公式可以得到该事件的概率为
,则列出从6个社区中选取两个的所有基本事件数为15,在所有的基本事件中找出满足至少有一个来自A社区的基本事件数为9,再根据古典概型的概率计算公式可以得到该事件的概率为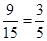 .
.
试题解析:
(1)社区总数为12+18+6=36,样本容量与总体中的个体数比为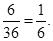
所以从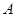 ,
,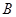 ,
,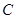 三个行政区中应分别抽取的社区个数为2,3,1. 4分
三个行政区中应分别抽取的社区个数为2,3,1. 4分
(2)设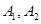 为在
为在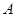 行政区中抽得的2个社区,
行政区中抽得的2个社区,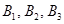 为在B行政区中抽得的3个社区,
为在B行政区中抽得的3个社区,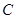 为在
为在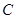 行政区中抽得的社区,在这6个社区中随机抽取2个,全部可能的结果有
行政区中抽得的社区,在这6个社区中随机抽取2个,全部可能的结果有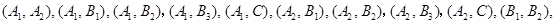
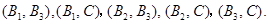 共有15种. 7分
共有15种. 7分
设事件“抽取的2个社区至少有1个来自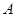 行政区”为事件
行政区”为事件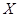 ,则事件
,则事件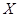 所包含的
所包含的
所有可能的结果有: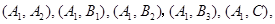
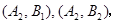
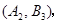
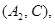
共有9种, 10分
以这2个社区中至少有1个来自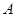 行政区的概率为
行政区的概率为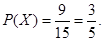 12分
12分
考点:分层抽样古典概型


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:解答题
根据以往的经验,某工程施工期间的降水量X(单位:mm)对工期的影响如下表:
| 降水量X | 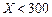 | 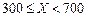 | 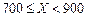 | 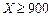 |
工期延误天数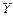 | 0 | 2 | 6 | 10 |
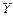 的均值与方差;(2)在降水量X至少是300的条件下,工期延误不超过6天的概率.
的均值与方差;(2)在降水量X至少是300的条件下,工期延误不超过6天的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在0,1,2,3,…,9这十个自然数中,任取三个不同的数字.将取出的三个数字按从小到大的顺序排列,设ξ为三个数字中相邻自然数的组数(例如:若取出的三个数字为0,1,2,则相邻的组为0,1和1,2,此时ξ的值是2),求随机变量ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市公租房的房源位于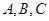 三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的任4位申请人中:
三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的任4位申请人中:
(1)恰有2人申请 片区房源的概率;
片区房源的概率;
(2)申请的房源所在片区的个数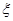 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商店试销某种商品20天,获得如下数据:
| 日销售量(件) | 0 | 1 | 2 | 3 |
| 频数 | 1 | 5 | 9 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校举行中学生“日常生活小常识”知识比赛,比赛分为初赛和复赛两部分,初赛采用选手从备选题中选一题答一题的方式进行;每位选手最多有5次答题机会,选手累计答对3题或答错3题即终止比赛,答对3题者直接进入复赛,答错3题者则被淘汰.已知选手甲答对每个题的概率均为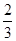 ,且相互间没有影响.
,且相互间没有影响.
(1)求选手甲进入复赛的概率;
(2)设选手甲在初赛中答题的个数为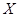 ,试求
,试求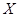 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个口袋中有 个白球和
个白球和 个红球(
个红球( ,且
,且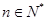 ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(1)试用含 的代数式表示一次摸球中奖的概率
的代数式表示一次摸球中奖的概率 ;
;
(2)若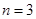 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;
(3)记三次摸球恰有一次中奖的概率为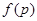 ,当
,当 为何值时,
为何值时,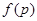 取最大值.
取最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在高中“自选模块”考试中,某考场的每位同学都选了一道数学题,第一小组选《数学史与不等式选讲》的有1人,选《矩阵变换和坐标系与参数方程》的有5人,第二小组选《数学史与不等式选讲》的有2人,选《矩阵变换和坐标系与参数方程》的有4人,现从第一、第二两小组各任选2人分析得分情况.
(1)求选出的4人均为选《矩阵变换和坐标系与参数方程》的概率;
(2)设X为选出的4个人中选《数学史与不等式选讲》的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知A、B、C三个箱子中各装有2个完全相同的球,每个箱子里的球,有一个球标着号码1,另一个球标着号码2,现从A、B、C三个箱子中各摸出1个球.
(1) 若用数组(x,y,z)中的x、y、z分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组(x,y,z)的所有情形,并回答一共有多少种;
(2) 如果猜测摸出的这三个球的号码之和,猜中有奖,那么猜什么数获奖的可能性最大?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com