练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    动点P到点M(1，0)及点N(3，0)的距离之差为2，则点P的轨迹是

    [　　]
    A．

    双曲线

    B．

    双曲线的一支

    C．

    两条射线

    D．

    一条射线

    答案：D
    解析：

    |PM|－|PN|＝2，而|MN|＝2，所以P在线段MN的延长线上．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：学习周报　数学　人教课标高二版(A选修1－1)　2009－2010学年　第18期　总第174期 人教课标版(A选修1－1) 题型：013

    动点P到点M(1，0)及点N(3，0)的距离之差为2，则点P的轨迹是

    [　　]
    A．

    双曲线

    B．

    双曲线的一支

    C．

    两条射线

    D．

    一条射线

    查看答案和解析>>

    科目：高中数学 来源：山东省潍坊市2012届高三下学期考前仿真模拟(五)数学文科试题 题型：022

    下列四个命题：

    ①若m∈(0，1]，则函数的最小值为；

    ②已知平面α，β，直线l，m，若l⊥α，mβ，α⊥β，则l∥m；

    ③△ABC中，和的夹角等于180°－A；

    ④若动点P到点F(1，0)的距离比到直线l：x＝－2的距离小1，则动点P的轨迹方程为．

    其中正确命题的序号为________．

    查看答案和解析>>

    科目：高中数学 来源：重庆市重庆八中2011届高三第七次月考数学文科试题 题型：044

    动点P到点F(1，0)的距离与它到直线l：x＝－1的距离相等，记点P的轨迹为曲线C1．圆C2的圆心T是曲线C1上的动点，圆C2与y轴交于M，N两点，且|MN|＝4．

    (Ⅰ)求曲线C1的方程；

    (Ⅱ)设点A(a，0)(a＞2)，若点A到点T的最短距离为a－1，试判断直线l与圆C2的位置关系，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源：江西省高考真题 题型：解答题

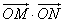    设动点P到点A(-1，0)和B(1，0)的距离分别为d1和d2，∠APB=2θ，且存在常数λ(0＜λ＜1)，使得d1d2sin2θ=λ，
    （1）证明：动点P的轨迹C为双曲线，并求出C的方程；
    （2）过点B作直线交双曲线C的右支于M、N两点，试确定λ的范围，使=0，其中点O为坐标原点．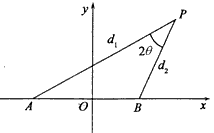

    查看答案和解析>>

    同步练习册答案