n
2-2n+3
分析:由三角形数阵看出,从第三行开始起,每一行的第二个数与它前一行的第二个数的差构成以2为公差的等差数列,然后利用累加的办法求得第n行的第二个数.
解答:由图看出a
(2,2)=3,a
(3,2)=6,a
(4,2)=11,a
(5,2)=18.
由此看出a
(3,2)-a
(2,2)=3,
a
(4,2)-a(3,2)=5,
a
(5,2)-a
(4,2)=7,
…
a
(n,2)-a
(n-1,2)=2n-3.
以上n-2个式子相加得:a
(n,2)-a
(2,2)=3+5+7+…+(2n-3)=
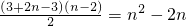
.
所以
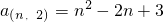
.
故答案为n
2-2n+3.
点评:本题考查了类比推理,考查了数列的函数特性,解答此题的关键是找出有效的规律,即从第三行开始起,每一行的第二个数与它前一行的第二个数的差构成以2为公差的等差数列,此题是中档题型.

 如图,一个类似杨辉三角的数阵,请写出第n(n≥2)行的第2个数为________.
如图,一个类似杨辉三角的数阵,请写出第n(n≥2)行的第2个数为________.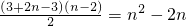 .
.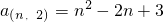 .
.

 名校课堂系列答案
名校课堂系列答案