
若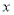 ,
,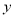 满足约束条件
满足约束条件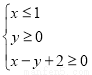 ,则
,则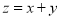 的最大值为 .
的最大值为 .
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试理科数学试卷(解析版) 题型:解答题
如图,在四棱锥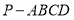 中,
中,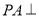 平面
平面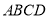 ,底面
,底面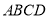 是直角梯形,
是直角梯形,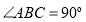 ,
,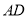 ∥
∥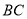 ,且
,且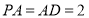 ,
,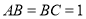 ,
, 为
为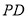 的中点.
的中点.

(1)设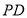 与平面
与平面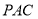 所成的角为
所成的角为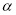 ,二面角
,二面角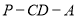 的大小为
的大小为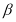 ,求证:
,求证: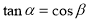 ;
;
(2)在线段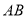 上是否存在一点
上是否存在一点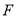 (与
(与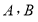 两点不重合),使得
两点不重合),使得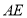 ∥平面
∥平面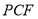 ? 若存在,求
? 若存在,求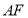 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试理科数学试卷(解析版) 题型:选择题
下列说法错误的是( )
A.命题“若x2-5x+6=0,则x=2”的逆否命题是“若x≠2,则x2-5x+6≠0”
B.已知命题p和q,若p∨q为假命题,则命题p与q中必一真一假
C.若x,y∈R,则“x=y”是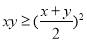 的充要条件
的充要条件
D.若命题p: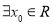 ,
,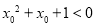 则
则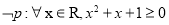
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试文科数学试卷(解析版) 题型:填空题
将长度为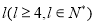 的线段分成
的线段分成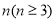 段,每段长度均为正整数,并要求这
段,每段长度均为正整数,并要求这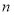 段中的任意三段都不能构成三角形.例如,当
段中的任意三段都不能构成三角形.例如,当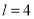 时,只可以分为长度分别为1,1,2的三段,此时
时,只可以分为长度分别为1,1,2的三段,此时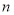 的最大值为3;当
的最大值为3;当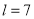 时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时
时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时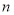 的最大值为4.则:
的最大值为4.则:
(1)当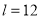 时,
时,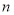 的最大值为________;
的最大值为________;
(2)当 时,
时,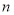 的最大值为________.
的最大值为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试文科数学试卷(解析版) 题型:选择题
角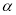 顶点在坐标原点
顶点在坐标原点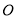 ,始边与
,始边与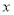 轴的非负半轴重合,
轴的非负半轴重合, ,点
,点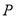 在
在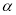 的终边上,点
的终边上,点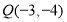 ,则
,则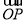 与
与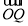 夹角余弦值为( )
夹角余弦值为( )
A.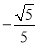 B.
B.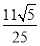 C.
C.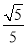 或
或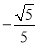 D.
D.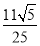 或
或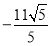
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(二)理科数学试卷(解析版) 题型:解答题
已知函数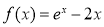 ,
,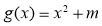 (
(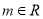 )
)
(1)对于函数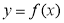 中的任意实数x,在
中的任意实数x,在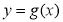 上总存在实数
上总存在实数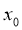 ,使得
,使得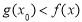 成立,求实数
成立,求实数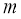 的取值范围
的取值范围
(2)设函数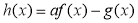 ,当
,当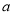 在区间
在区间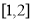 内变化时,
内变化时,
(1)求函数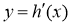
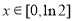 的取值范围;
的取值范围;
(2)若函数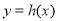
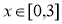 有零点,求实数m的最大值.
有零点,求实数m的最大值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(二)理科数学试卷(解析版) 题型:选择题
李先生居住在城镇的A处,准备开车到单位B处上班,途中(不绕行)共要经过6个交叉路口,假设每个交叉路口发生堵车事件的概率均为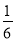 ,则李先生在一次上班途中会遇到堵车次数
,则李先生在一次上班途中会遇到堵车次数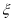 的期望值
的期望值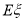 是( )
是( )
A.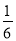 B.1 C.
B.1 C.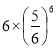 D.
D.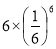
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com