
如图,在四棱锥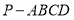 中,
中,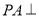 平面
平面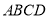 ,底面
,底面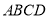 是直角梯形,
是直角梯形,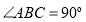 ,
,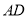 ∥
∥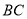 ,且
,且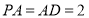 ,
,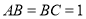 ,
,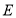 为
为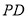 的中点.
的中点.

(1)设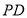 与平面
与平面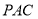 所成的角为
所成的角为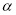 ,二面角
,二面角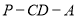 的大小为
的大小为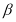 ,求证:
,求证: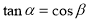 ;
;
(2)在线段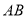 上是否存在一点
上是否存在一点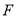 (与
(与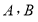 两点不重合),使得
两点不重合),使得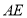 ∥平面
∥平面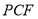 ? 若存在,求
? 若存在,求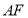 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
(1)详见解析;(2)存在,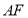 的长为
的长为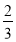 .
.
【解析】
试题分析:(1)直线和平面所成的角以及二面角的计算,可以考虑两种方法,其一利用传统立体几何的方法,由已知得,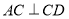 ,又
,又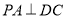 ,故
,故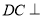 面
面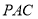 ,则
,则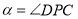 ,由
,由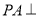 平面
平面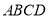 ,
,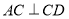 ,故
,故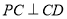 ,则
,则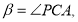 ,然后分别在直角三角形中,求
,然后分别在直角三角形中,求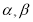 ,或者可以建立空间直角坐标系,通过平面的法向量和直线的方向向量求直线和平面所成的角,利用两个半平面的法向量来求二面角的大小;(2)建立空间直角坐标系,设点
,或者可以建立空间直角坐标系,通过平面的法向量和直线的方向向量求直线和平面所成的角,利用两个半平面的法向量来求二面角的大小;(2)建立空间直角坐标系,设点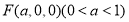 ,并求出半平面
,并求出半平面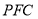 的法向量,利用
的法向量,利用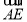 和法向量垂直,列等式,即可求解.
和法向量垂直,列等式,即可求解.

试题解析:解法一:(1)证明: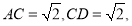 又
又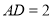
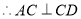 1分
1分
又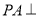 平面
平面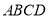 ,
,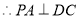 ,
,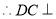 面
面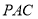 2分
2分
∴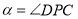
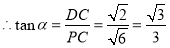 3分
3分
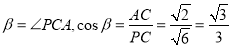 , 5分
, 5分

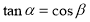 6分
6分
(2)取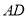 的中点
的中点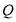 ,连
,连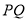 交
交 于
于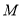 ,由
,由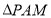 与
与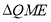 相似得,
相似得,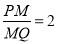 , 7分
, 7分
在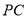 上取点
上取点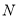 ,使
,使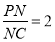 ,则
,则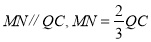 , 8分
, 8分
在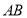 上取点
上取点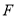 使
使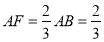 ,由于
,由于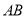 平行且等于
平行且等于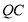 ,
,
故有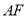 平行且等于
平行且等于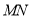 , 9分
, 9分
四边形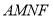 为平行四边形,所以
为平行四边形,所以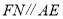 , 10分
, 10分
而 , 故有
, 故有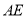 ∥平面
∥平面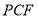 , 11分
, 11分
所以在线段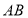 上存在一点
上存在一点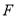 使得
使得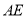 ∥平面
∥平面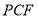 ,
,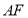 的长为
的长为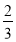 . 12分
. 12分
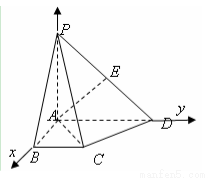
解法二:(1)同解法一;
(2)如图,以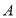 为原点,
为原点,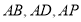 所在直线分别为
所在直线分别为 轴,建立直角坐标系,则
轴,建立直角坐标系,则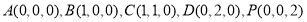 ,
,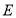 为
为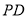 的中点,则
的中点,则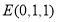 7分
7分
假设存在符合条件的点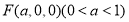 ,则
,则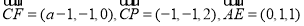 共面,
共面,
故存在实数 ,使得
,使得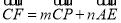 9分
9分
即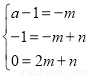 ,故有
,故有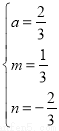 即
即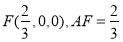 11分
11分
即存在符合条件的点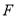 ,
,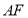 的长为
的长为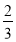 . 12分
. 12分
考点:1、直线和平面所成的角;2、二面角的求法;3、直线和平面平行的判定.


科目:高中数学 来源:2013-2014学年湖北省武汉市高三下学期4月调研测试文科数学试卷(解析版) 题型:选择题
若一元二次不等式 对一切实数
对一切实数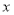 都成立,则
都成立,则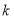 的取值范围为( )
的取值范围为( )
A.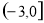 B.
B.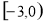 C.
C.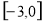 D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省天门市毕业生四月调研考试理科数学试卷(解析版) 题型:选择题
函数 的零点所在区间为( )
的零点所在区间为( )
A.(0,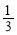 ) B.(
) B.(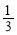 ,
,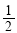 ) C.(
) C.(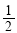 ,1) D.(1,2)
,1) D.(1,2)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省天门市毕业生四月调研考试文科数学试卷(解析版) 题型:选择题
设平面向量 ,
,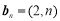 ,其中
,其中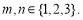 记“使得
记“使得 成立的
成立的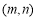 ”为事件A,则事件A发生的概率为( )
”为事件A,则事件A发生的概率为( )
A. B.
B. C.
C.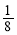 D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省天门市毕业生四月调研考试文科数学试卷(解析版) 题型:选择题
下图是根据变量x,y的观测数据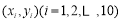 得到的散点图,由这些散点图可以判断变量x,y具有相关关系的图是( )
得到的散点图,由这些散点图可以判断变量x,y具有相关关系的图是( )
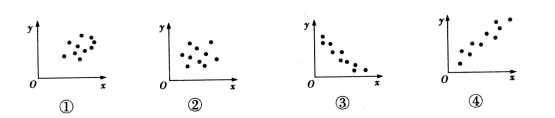
A.①② B.①④ C.②③ D.③④
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试理科数学试卷(解析版) 题型:填空题
将长度为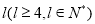 的线段分成
的线段分成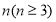 段,每段长度均为正整数,并要求这
段,每段长度均为正整数,并要求这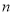 段中的任意三段都不能构成三角形.例如,当
段中的任意三段都不能构成三角形.例如,当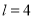 时,只可以分为长度分别为1,1,2的三段,此时
时,只可以分为长度分别为1,1,2的三段,此时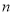 的最大值为3;当
的最大值为3;当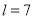 时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时
时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时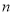 的最大值为4.则:
的最大值为4.则:
(1)当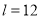 时,
时, 的最大值为________;(2)当
的最大值为________;(2)当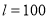 时,
时,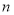 的最大值为________.
的最大值为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试理科数学试卷(解析版) 题型:选择题
已知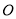 为坐标原点,
为坐标原点,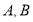 两点的坐标均满足不等式组
两点的坐标均满足不等式组 设
设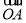 与
与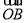 的夹角为
的夹角为
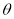 ,则
,则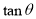 的最大值为 ( )
的最大值为 ( )
A.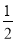 B.
B.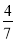 C.
C.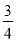 D.
D.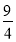
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com