
完成下列问题.
(1)求等式![]() 中的n值;
中的n值;
(2)若![]() ,则n的解集为__________;
,则n的解集为__________;
(3)已知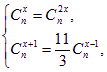 试求x、n的值.
试求x、n的值.
(1)原方程可变形为
![]()
![]()
化简整理得n2-3n-54=0.
解此二次方程得n=9或n=-6(不合题意,舍去),所以n=9为所求.
(2)由![]()
![]()
可得n2-11n-12<0.解得-1<n<12.
又∵n∈N*,且n≥5,∴n∈{5,6,7,8,9,10,11}.
(3)∵![]()
∴n-x=2x或x=2x(舍去).∴n=3x.
又由![]()
整理得3(x-1)!(n-x+1)!=11(x+1)!(n-x-1)!,
3(n-x+1)(n-x)=11(x+1)x.将n=3x代入,
整理得6(2x+1)=11(x+1).
∴x=5,n=3x=15.
(1)本题实质是解一个关于n的方程,但要注意对根的限制条件;
(2)将组合数不等式转化为代数不等式来解;
(3)本题是关于x、n的二元方程组,解此方程组,方程组的解要满足限制条件.


科目:高中数学 来源: 题型:
探究函数![]() ,x∈(0,+∞)的最小值,并确定相应的x的值,列表如下:
,x∈(0,+∞)的最小值,并确定相应的x的值,列表如下:
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
请观察表中y值随x值变化的特点,完成下列问题:
(1)若函数![]() ,(x>0)在区间(0,2)上递减,则在 上递增;
,(x>0)在区间(0,2)上递减,则在 上递增;
(2)当x= 时,![]() ,(x>0)的最小值为 ;
,(x>0)的最小值为 ;
(3)试用定义证明![]() ,(x>0)在区间(0,2)上递减;
,(x>0)在区间(0,2)上递减;
(4)函数![]() ,(x<0)有最值吗?是最大值还是最小值?此时x为何值?
,(x<0)有最值吗?是最大值还是最小值?此时x为何值?
(5)解不等式![]() .
.
解题说明:(1)(2)两题的结果直接填写在横线上;(4)题直接回答,不需证明。
查看答案和解析>>
科目:高中数学 来源:2015届福建省高一上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分13分)某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品 (百台),其总成本为
(百台),其总成本为 (万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为2万元(总成本=固定成本+生产成本).销售收入
(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为2万元(总成本=固定成本+生产成本).销售收入 (万元)满足
(万元)满足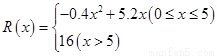 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出函数 的解析式;
的解析式;
(2)写出利润函数 的解析式(利润=销售收入—总成本);
的解析式(利润=销售收入—总成本);
(3)工厂生产多少台产品时,可使盈利最多?
查看答案和解析>>
科目:高中数学 来源:2010年河北省高一上学期期中考试数学试卷 题型:解答题
(本题满分12分)探究函数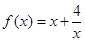 ,
,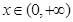 的最小值,并确定取得最小值时
的最小值,并确定取得最小值时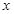 的值,列表如下:
的值,列表如下:
|
|
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
|
|
… |
8.5 |
5 |
4.17 |
4.05 |
4.005 |
4 |
4.005 |
4.102 |
4.24 |
4.3 |
5 |
5.8 |
7.57 |
… |
请观察表中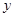 值随
值随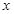 值变化的特点,完成下列问题:
值变化的特点,完成下列问题:
(1) 当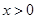 时,
时,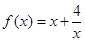 在区间
在区间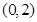 上递减,在区间 上递增;
上递减,在区间 上递增;
所以,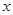 =
时,
=
时, 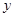 取到最小值为
;
取到最小值为
;
(2) 由此可推断,当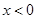 时,
时,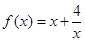 有最
值为 ,此时
有最
值为 ,此时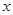 =
;
=
;
(3) 证明: 函数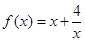 在区间
在区间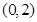 上递减;
上递减;
(4) 若方程 在
在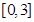 内有两个不相等的实数根,求实数
内有两个不相等的实数根,求实数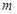 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
(2)小明要从教学楼的底层上到三层,已知从底层到二层有4个扶梯可走,从二层到三层有2个扶梯可走,问小明从底层到三层的走法共有几种?
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分15分)
某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为2万元(总成本=固定成本+生产成本).销售收入
(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为2万元(总成本=固定成本+生产成本).销售收入![]() (万元)满足
(万元)满足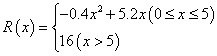 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数![]() 的解析式(利润=销售收入—总成本)
的解析式(利润=销售收入—总成本)
(2)工厂生产多少台产品时,可使盈利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com